Question

Find intervals for which f is increasing and decreasing, local max and local min, concavity and inflection points?
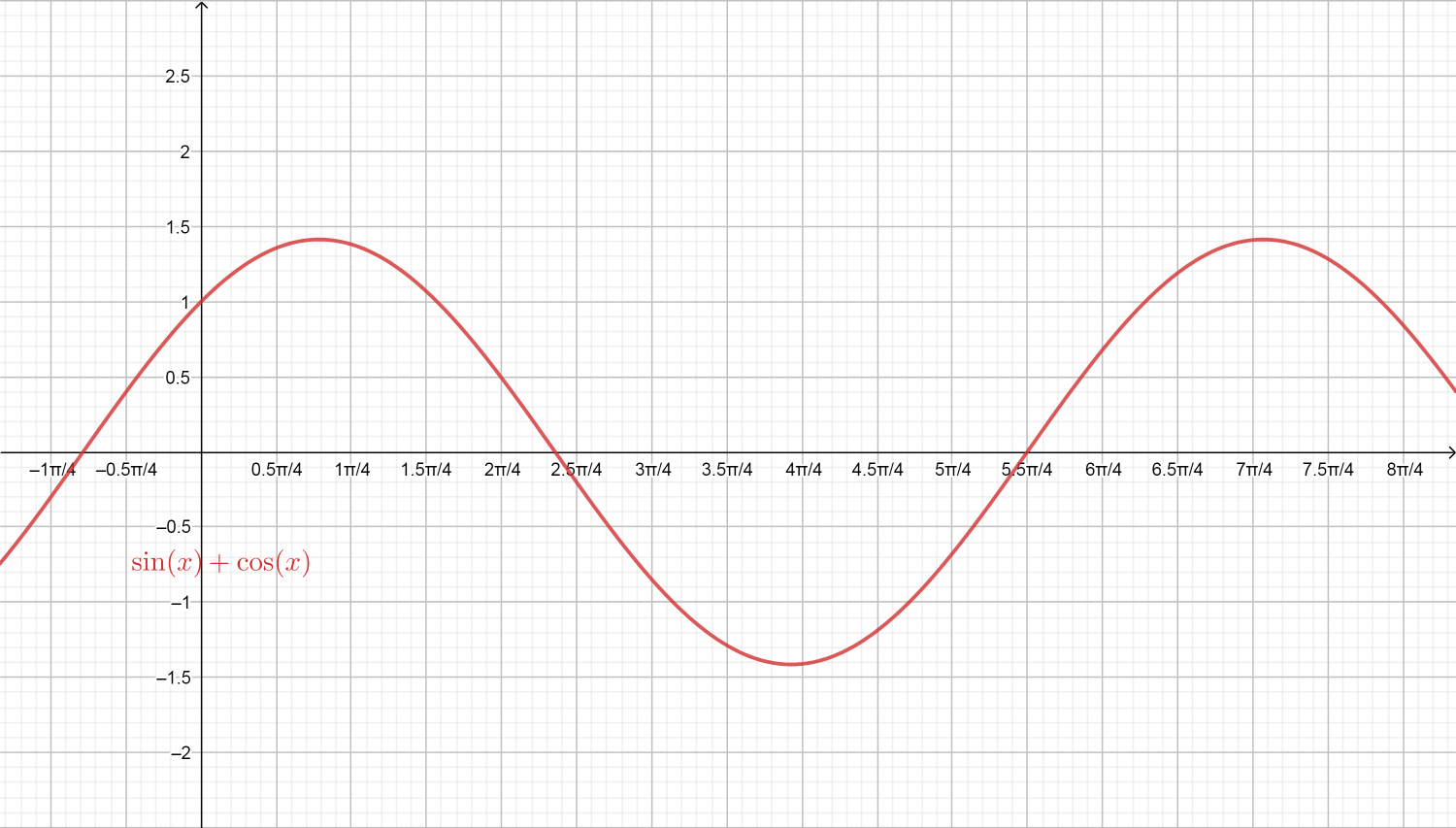
$f\left( x \right) = \sin x + \cos x,\left[ {0,2\pi } \right]$

Answer 1

In the above given problem, we are given a trigonometric function which is the sum of two trigonometric functions, the sine and cosine functions. The interval of this function is given as $\left[ {0,2\pi } \right]$ . We have to find the intervals in which f is increasing and decreasing, the local maxima and local minima, its concavity and the inflection points for the given function. We can approach the required solutions by using the first and second derivative methods.

Complete answer:
Given trigonometric function is $f\left( x \right) = \sin x + \cos x$ .
The interval of this function is given as $\left[ {0,2\pi } \right]$ .
We have to find the increasing and decreasing intervals of this function along with the local minima and maxima, concavity and inflection points.
We can approach them using the method of first and second derivative tests.
Since the function is,
$\Rightarrow f\left( x \right) = \sin x + \cos x$
Hence, differentiating the function once gives us,
$\Rightarrow f'\left( x \right) = \cos x - \sin x$
For the inflection points of a function, we have $f'\left( x \right) = 0$ , that gives us the equation as
$\Rightarrow f'\left( x \right) = \cos x - \sin x = 0$
Hence,
$\Rightarrow \cos x = \sin x$
That gives us two values in the interval which satisfy the above condition,
$\Rightarrow x = \dfrac{\pi }{4},\dfrac{{5\pi }}{4} \in \left[ {0,2\pi } \right]$
These are the critical points.
Now, the second derivative of the function is given by,
$\Rightarrow f''\left( x \right) = - \left( {\sin x + \cos x} \right)$
Now, at $x = \dfrac{\pi }{4}$ we have,
$\Rightarrow f''\left( x \right) = - 1 < 0$
Hence it has local maxima at $x = \dfrac{\pi }{4}$ .
That is,
$\Rightarrow f\left( {\dfrac{\pi }{4}} \right) = \sin \left( {\dfrac{\pi }{4}} \right) + \cos \left( {\dfrac{\pi }{4}} \right) = 1$
Also, at $x = \dfrac{{5\pi }}{4}$ , we have
$\Rightarrow f''\left( x \right) = 1 > 0$
Hence it has local minima at $x = \dfrac{{5\pi }}{4}$ .
That is,
$\Rightarrow f\left( {\dfrac{{5\pi }}{4}} \right) = \sin \left( {\dfrac{{5\pi }}{4}} \right) + \cos \left( {\dfrac{{5\pi }}{4}} \right) = - 1$
Now, we have to check the nature of the function after $0,\dfrac{\pi }{4},\dfrac{{5\pi }}{4}$ .
The sign chart for the function $f\left( x \right) = \sin x + \cos x$ can be shown as:

Interval	Sign of	Nature of $f\left( x \right)$
$\left[ {0,\left. {\dfrac{\pi }{4}} \right)} \right.$	negative	Increasing
$\left( {\dfrac{\pi }{4},\dfrac{{5\pi }}{4}} \right)$	positive	Decreasing
$\left( {\dfrac{{5\pi }}{4}} \right.,\left. {2\pi } \right]$	negative	Increasing

Now for the concavity of $f\left( x \right) = \sin x + \cos x$ , we have $f''\left( x \right) = 0$ , that gives us

That gives,
$\Rightarrow \sin x = - \cos x$
The values which satisfy above condition are,
$\Rightarrow x = \dfrac{{3\pi }}{4},\dfrac{{7\pi }}{4}$
These are the inflection points.
Again, the sign chart for the concavity of the function $f\left( x \right) = \sin x + \cos x$ can be shown as:

Interval	Sign of	Concavity
$\left[ 0 \right.,\left. {\dfrac{{3\pi }}{4}} \right)$	Negative	Concave Down
$\left( {\dfrac{{3\pi }}{4},\dfrac{{7\pi }}{4}} \right)$	Positive	Concave Up
$\left( {\dfrac{{7\pi }}{4},\left. {2\pi } \right]} \right.$	Negative	Concave Down

Note: We can also draw the graph of the function $f\left( x \right) = \sin x + \cos x$ which shows the concavity and as well as the increasing decreasing nature of the given trigonometric function.