Question

find integral roots of eq $x^2+ax+a+1=0$ and also find integral values of a.

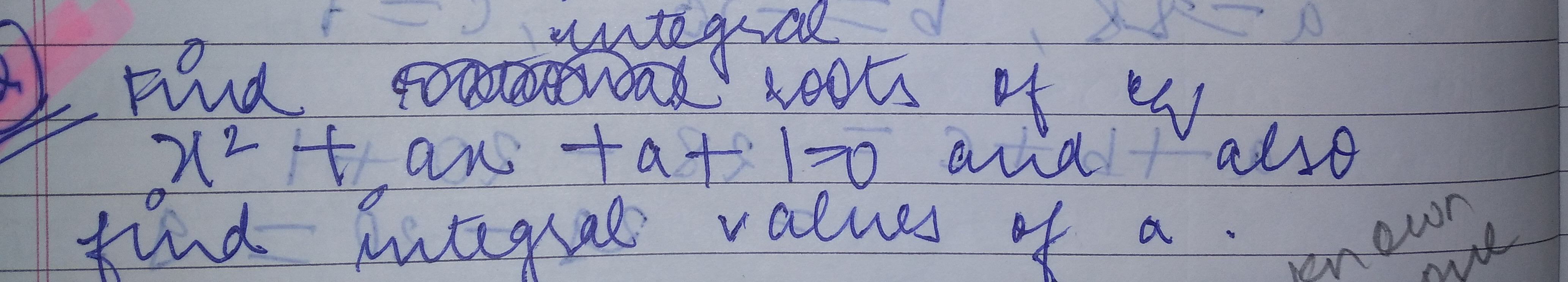
Answer 1

Integral roots are $0, 1, -2, -3$. Integral values of $a$ are $-1, 5$.

Answer 2

Let the integral roots be $x_1$ and $x_2$. From Vieta's formulas: $x_1 + x_2 = -a$ $x_1 x_2 = a + 1$

Substituting $a = -(x_1 + x_2)$ into the second equation: $x_1 x_2 = -(x_1 + x_2) + 1$ $x_1 x_2 + x_1 + x_2 = 1$ Adding 1 to both sides: $(x_1 + 1)(x_2 + 1) = 2$

The integer factor pairs of 2 are $(1, 2)$ and $(-1, -2)$.

Case 1: $x_1 + 1 = 1, x_2 + 1 = 2 \implies x_1 = 0, x_2 = 1$. $a = -(0 + 1) = -1$.

Case 2: $x_1 + 1 = -1, x_2 + 1 = -2 \implies x_1 = -2, x_2 = -3$. $a = -(-2 + -3) = 5$.

The integral roots are $0, 1, -2, -3$. The integral values of $a$ are $-1, 5$.