Question

Find : $\int \frac{x^2-x+1}{(x-1)(x^2+1)} dx$

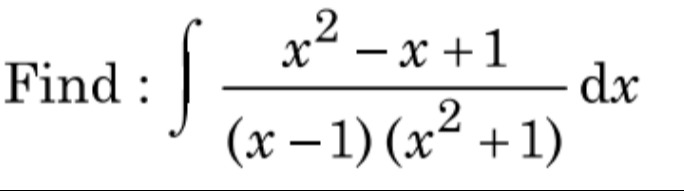
Answer 1

$\frac{1}{2} \ln|x-1| + \frac{1}{4} \ln(x^2+1) - \frac{1}{2} \arctan(x) + C$

Answer 2

We use partial fraction decomposition: $\frac{x^2-x+1}{(x-1)(x^2+1)} = \frac{A}{x-1} + \frac{Bx+C}{x^2+1}$ Solving for constants gives $A=\frac{1}{2}$, $B=\frac{1}{2}$, $C=-\frac{1}{2}$. The integral becomes: $\int \left(\frac{1}{2(x-1)} + \frac{x-1}{2(x^2+1)}\right) dx$ Integrating term-wise: $\frac{1}{2}\int\frac{dx}{x-1} + \frac{1}{2}\int\frac{x}{x^2+1}dx - \frac{1}{2}\int\frac{1}{x^2+1}dx$ $= \frac{1}{2}\ln|x-1| + \frac{1}{4}\ln(x^2+1) - \frac{1}{2}\arctan(x) + C$