Solveeit Logo
Login

Question

Question: Find instant at which average velocity of First & second = instantaneous velocity at t th second (Po...

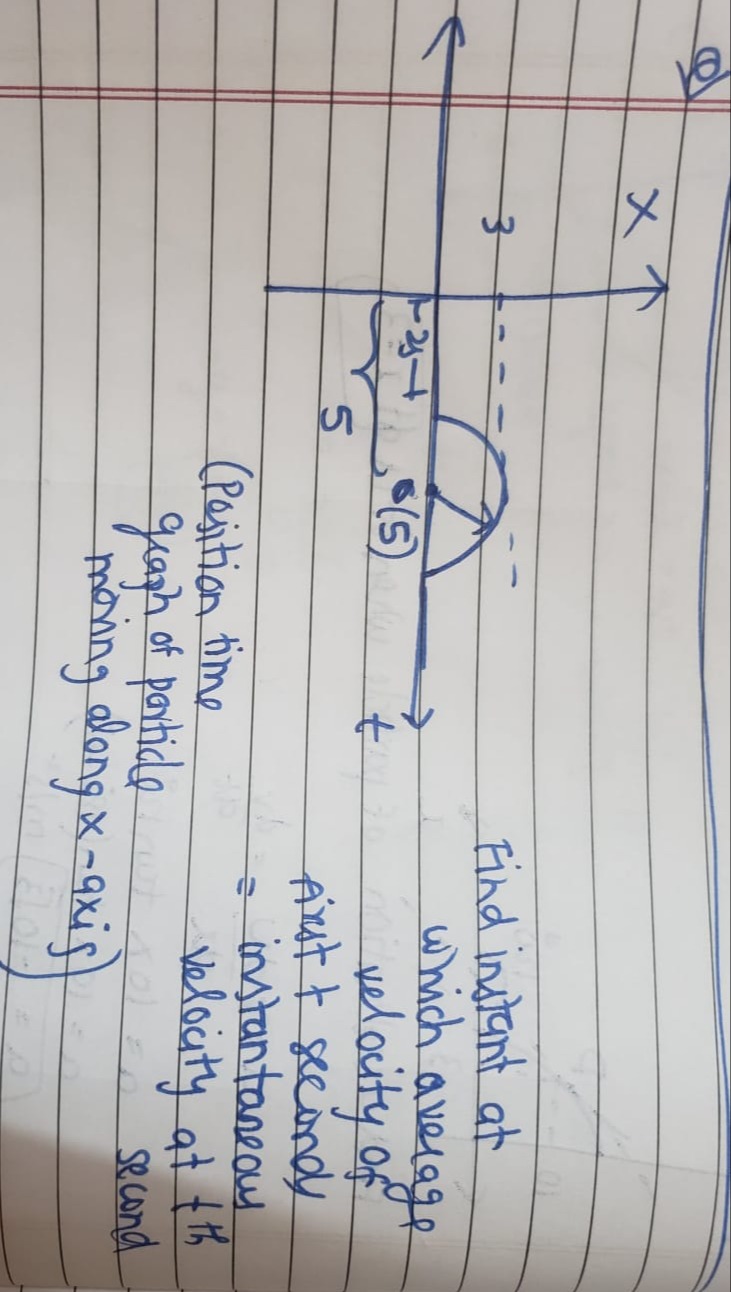
Find instant at which average velocity of First & second = instantaneous velocity at t th second (Position time graph of portide moving along x-axis)

Answer

3.2 seconds

Explanation

Solution

The problem asks for the instant t at which the average velocity from the beginning of the motion (assumed to be t=0) to time t is equal to the instantaneous velocity at time t. The position-time graph is a semicircle.

1. Analyze the Position-Time Graph: The graph shows a semicircle in the x-t plane.

  • The x-axis represents time (t).
  • The y-axis represents position (x).
  • The semicircle starts at t=2 and ends at t=8.
  • The center of the semicircle is at t = (2+8)/2 = 5. Since the semicircle is centered on the t-axis (x=0), the center coordinates are C = (5, 0).
  • The radius of the semicircle is R = (8-2)/2 = 3.
  • The semicircle is drawn below the t-axis, meaning the position x is negative for points on the semicircle (except at t=2 and t=8 where x=0).
  • The equation of the semicircle is (t−5)2+x2=R2(t-5)^2 + x^2 = R^2, which is (t−5)2+x2=32=9(t-5)^2 + x^2 = 3^2 = 9.
  • Since x is negative, x(t)=−9−(t−5)2x(t) = -\sqrt{9 - (t-5)^2} for 2≤t≤82 \le t \le 8.

2. Define Average and Instantaneous Velocity:

  • Average velocity from t=0 to t: Assuming the particle starts at x=0 at t=0, the average velocity is vavg=x(t)−x(0)t−0=x(t)tv_{avg} = \frac{x(t) - x(0)}{t - 0} = \frac{x(t)}{t}.
  • Instantaneous velocity at t: This is the derivative of position with respect to time, vinst=dxdtv_{inst} = \frac{dx}{dt}.

3. Set up the Condition: We need to find t such that vavg=vinstv_{avg} = v_{inst}, i.e., x(t)t=dxdt\frac{x(t)}{t} = \frac{dx}{dt}.

4. Calculate dxdt\frac{dx}{dt}: Given x(t)=−9−(t−5)2=−[9−(t−5)2]1/2x(t) = -\sqrt{9 - (t-5)^2} = -[9 - (t-5)^2]^{1/2}. Using the chain rule: dxdt=−12[9−(t−5)2]−1/2⋅ddt(9−(t−5)2)\frac{dx}{dt} = -\frac{1}{2}[9 - (t-5)^2]^{-1/2} \cdot \frac{d}{dt}(9 - (t-5)^2) dxdt=−12[9−(t−5)2]−1/2⋅(−2(t−5))\frac{dx}{dt} = -\frac{1}{2}[9 - (t-5)^2]^{-1/2} \cdot (-2(t-5)) dxdt=t−59−(t−5)2\frac{dx}{dt} = \frac{t-5}{\sqrt{9 - (t-5)^2}} Since x(t)=−9−(t−5)2x(t) = -\sqrt{9 - (t-5)^2}, we can write 9−(t−5)2=−x(t)\sqrt{9 - (t-5)^2} = -x(t). So, dxdt=t−5−x(t)\frac{dx}{dt} = \frac{t-5}{-x(t)}.

5. Solve the Equation x(t)t=dxdt\frac{x(t)}{t} = \frac{dx}{dt}: Substitute the expressions for x(t)x(t) and dxdt\frac{dx}{dt}: x(t)t=t−5−x(t)\frac{x(t)}{t} = \frac{t-5}{-x(t)} Cross-multiply: −x(t)2=t(t−5)-x(t)^2 = t(t-5) From the equation of the semicircle, x(t)2=9−(t−5)2x(t)^2 = 9 - (t-5)^2. Substitute this into the equation: −(9−(t−5)2)=t(t−5)-(9 - (t-5)^2) = t(t-5) −9+(t−5)2=t(t−5)-9 + (t-5)^2 = t(t-5) Expand (t−5)2(t-5)^2: −9+(t2−10t+25)=t2−5t-9 + (t^2 - 10t + 25) = t^2 - 5t t2−10t+16=t2−5tt^2 - 10t + 16 = t^2 - 5t Subtract t2t^2 from both sides: −10t+16=−5t-10t + 16 = -5t Add 10t10t to both sides: 16=5t16 = 5t t=165t = \frac{16}{5} t=3.2t = 3.2 seconds.

6. Verify the Solution: The obtained time t=3.2 seconds is within the domain of the semicircle, which is 2≤t≤82 \le t \le 8. At t=3.2t=3.2: x(3.2)=−9−(3.2−5)2=−9−(−1.8)2=−9−3.24=−5.76=−2.4x(3.2) = -\sqrt{9 - (3.2-5)^2} = -\sqrt{9 - (-1.8)^2} = -\sqrt{9 - 3.24} = -\sqrt{5.76} = -2.4. vavg=x(3.2)3.2=−2.43.2=−2432=−34=−0.75v_{avg} = \frac{x(3.2)}{3.2} = \frac{-2.4}{3.2} = -\frac{24}{32} = -\frac{3}{4} = -0.75 units/sec. vinst=3.2−5−(−2.4)=−1.82.4=−1824=−34=−0.75v_{inst} = \frac{3.2-5}{-(-2.4)} = \frac{-1.8}{2.4} = -\frac{18}{24} = -\frac{3}{4} = -0.75 units/sec. The average velocity equals the instantaneous velocity at t=3.2t=3.2 seconds.

Alternative Geometric Approach: The condition x(t)t=dxdt\frac{x(t)}{t} = \frac{dx}{dt} means that the line connecting the origin (0,0)(0,0) to the point (t,x(t))(t, x(t)) on the curve is tangent to the curve at that point. For a circle (or semicircle), the tangent line at a point is perpendicular to the radius drawn to that point. Let O be the origin (0,0)(0,0), P be the point (t,x(t))(t, x(t)) on the semicircle, and C be the center of the semicircle (5,0)(5,0). Triangle OCP is a right-angled triangle with the right angle at P. The lengths of the sides are:

  • OC=(5−0)2+(0−0)2=5OC = \sqrt{(5-0)^2 + (0-0)^2} = 5 (distance from origin to center).
  • CP=R=3CP = R = 3 (radius of the semicircle).
  • OP=(t−0)2+(x−0)2=t2+x2OP = \sqrt{(t-0)^2 + (x-0)^2} = \sqrt{t^2 + x^2} (distance from origin to point P). By the Pythagorean theorem in △OCP\triangle OCP: OP2+CP2=OC2OP^2 + CP^2 = OC^2 (t2+x2)2+32=52(\sqrt{t^2 + x^2})^2 + 3^2 = 5^2 t2+x2+9=25t^2 + x^2 + 9 = 25 t2+x2=16t^2 + x^2 = 16 (Equation 1) The point P(t,x) is on the semicircle, so it satisfies the semicircle equation: (t−5)2+x2=9(t-5)^2 + x^2 = 9 (Equation 2) From Equation 2, x2=9−(t−5)2x^2 = 9 - (t-5)^2. Substitute this x2x^2 into Equation 1: t2+(9−(t−5)2)=16t^2 + (9 - (t-5)^2) = 16 t2+9−(t2−10t+25)=16t^2 + 9 - (t^2 - 10t + 25) = 16 t2+9−t2+10t−25=16t^2 + 9 - t^2 + 10t - 25 = 16 10t−16=1610t - 16 = 16 10t=3210t = 32 t=3.2t = 3.2 seconds.