Question

Find how the normal acceleration of the balloon varies as a function of the height of the ascent. Given the velocity in x-direction and y-direction are ${v_x} = ay$ and ${v_y} = {v_0}$ respectively and height of the ascent is $y$ .
A) ${\omega _n} = \dfrac{{a{v_0}}}{{\sqrt {1 + {{\left( {\dfrac{{{a_y}}}{{{v_0}}}} \right)}^2}} }}$
B) ${\omega _n} = \dfrac{{2a{v_0}}}{{\sqrt {1 + {{\left( {\dfrac{{{a_y}}}{{{v_0}}}} \right)}^2}} }}$
C) ${\omega _n} = \dfrac{{3a{v_0}}}{{2\sqrt {1 + {{\left( {\dfrac{{{a_y}}}{{{v_0}}}} \right)}^2}} }}$
D) ${\omega _n} = \dfrac{{a{v_0}}}{{2\sqrt {1 + {{\left( {\dfrac{{{a_y}}}{{{v_0}}}} \right)}^2}} }}$

Answer 1

The ascending balloon describes a curvilinear path and hence will have a vertical displacement as well as a horizontal displacement. The concept of instantaneous velocity can be used to obtain an equation of the path of motion of the balloon.

Formula used:
The normal acceleration of an object describing a curvilinear path is given by, ${\omega _n} = a{v_y}\sin \theta$ where $a$ is the net acceleration, ${v_y}$ is the component of velocity in the y-direction, and $\theta$ is the angle at which the object is directed.
The time taken for a body to cover a displacement $d$ is given by, $t = \dfrac{d}{v}$ where $v$ is the velocity of the body.

Complete step by step answer:
Step 1: Sketch a figure depicting the ascent of the balloon and list the marked parameters.

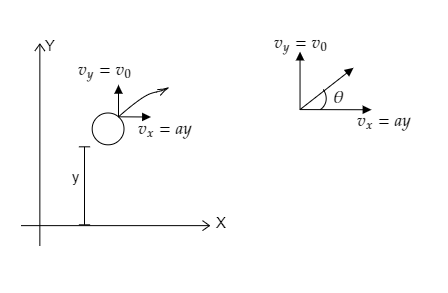
In the figure, the height of the ascent is $y$and the displacement of the balloon in the horizontal direction is $x$.
The velocity in the vertical direction is ${v_0}$ and that in the horizontal direction is ${v_x} = ay$ where $a$ is the total acceleration of the balloon and $y$ the height of the descent. The balloon is directed at an angle $\theta$ with the horizontal.
Step 2: Based on the concept of instantaneous velocity, the equation of the path described by the ascending balloon can be obtained.
Then the time taken to cover the vertical displacement will be, $t = \dfrac{y}{{{v_0}}}$
$\Rightarrow y = {v_0}t$ ------- (1)
The instantaneous velocity in the x-direction is given by, ${v_x} = \dfrac{{dx}}{{dt}}$ --------- (2)
Substituting for ${v_x} = ay$ in equation (2) we get,
$\Rightarrow ay = \dfrac{{dx}}{{dt}}$
$\Rightarrow dx = aydt$ -------- (3)
The horizontal displacement $x$ of the balloon is achieved in time $t$.
So equation (3) is integrated as $\int\limits_0^x {dx} = \int\limits_0^t {aydt}$
From equation (1) we have $y = {v_0}t$ and on substituting this in the above integral we get,
$\Rightarrow \int\limits_0^x {dx} = \int\limits_0^t {a{v_0}tdt} = a{v_0}\int\limits_0^t {tdt}$
On integrating and applying the limits, the above expression becomes,
$\Rightarrow x = a{v_0}\dfrac{{{t^2}}}{2}$ or $x = \dfrac{{a{y^2}}}{{2{v_0}}}$
The obtained equation suggests that the balloon has a parabolic path.
Step 3: Determine the vertical and horizontal component of the acceleration of the balloon to obtain an expression for the normal acceleration.
The acceleration in the x-direction is given by, ${a_x} = \dfrac{{d{v_x}}}{{dt}}$ .
Substituting for ${v_x} = a{v_0}t$ in the above relation we get,
$\Rightarrow {a_x} = \dfrac{{d\left( {a{v_0}t} \right)}}{{dt}} = a{v_0}$
So the acceleration in the x-direction is ${a_x} = a{v_0}$ .
However, the acceleration in the y-direction is zero i.e., ${a_y} = 0$ .
So the net acceleration will be equal to the acceleration in the x-direction i.e., $a = {a_x} = a{v_0}$
The normal acceleration of the balloon describing a parabolic path is given by,
${\omega _n} = a{v_0}\sin \theta$ -------- (4)
We know that $\sin \theta = \dfrac{{{\text{opposite side}}}}{{{\text{hypotenuse}}}}$ .
From the sketched figure, we have
$\Rightarrow \sin \theta = \dfrac{{{v_0}}}{{\sqrt {{v_0}^2 + {a_y}^2} }}$
Substituting for $\sin \theta = \dfrac{{{v_0}}}{{\sqrt {{v_0}^2 + {a_y}^2} }}$ in equation (4) we obtain
$\Rightarrow {\omega _n} = \dfrac{{a{v_0}^2}}{{\sqrt {{v_0}^2 + {a_y}^2} }}$
On simplifying, the above expression becomes
$\Rightarrow {\omega _n} = \dfrac{{a{v_0}^2}}{{{v_0}\sqrt {1 + {{\left( {\dfrac{{{a_y}}}{{{v_0}}}} \right)}^2}} }} = \dfrac{{a{v_0}}}{{\sqrt {1 + {{\left( {\dfrac{{{a_y}}}{{{v_0}}}} \right)}^2}} }}$

Therefore, the normal acceleration is given by, ${\omega _n} = \dfrac{{a{v_0}}}{{\sqrt {1 + {{\left( {\dfrac{{{a_y}}}{{{v_0}}}} \right)}^2}} }}$. So the correct option is A.

Note:
Here the rate of ascension is constant and so the acceleration in the y-direction will be zero. For parabola, $x \propto {y^2}$ and the equation obtained for the path of the balloon $x = \dfrac{{a{y^2}}}{{2{v_0}}}$ shows the same proportionality relation. The normal or radial acceleration describes how the direction of the velocity changes with time. It depends on the angle at which the balloon is directed, its net acceleration, and the component of velocity in the vertical direction.