Question
Question: Find force in newton which mass A exerts on mass B, if B is moving towards right with \(3m{{s}^{-2}}...
Find force in newton which mass A exerts on mass B, if B is moving towards right with 3ms−2 . Also find mass of A. (All surfaces are smooth,g=10ms−2)
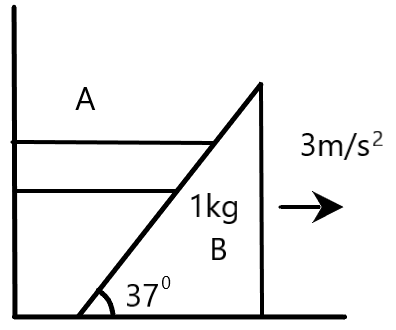
A)5N,3116kgB)10N,1631kgC)10N,3116kgD)5N,1631kg
Solution
Here we will consider the different forces acting on the body A and B. Then we will equate the component of forces in the horizontal direction to get the value of the force exerted by A. Then we will equate the components of acceleration along the normal of the inclined plane of B to get the acceleration of A. Lastly we will write the equation of motion of A in the vertical direction to get its mass.
Complete answer:
Let the force exerted by mass A on mass B along the normal of B is F. Then we have the diagram-
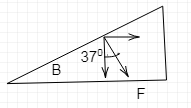
Now the mass B moves with the acceleration 3ms−2 towards the right. So, from the diagram we can write-
Fsin370=1×3⇒F=3×35=5N
This is the force which is exerted by the mass A on mass B. Same force is exerted by mass B on mass A. Now let a be the acceleration of A vertically downward. Now both the masses have the same acceleration along the normal. So we have the diagram-
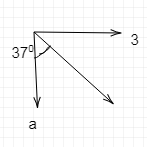
From the diagram we can write-
acos370=3cos530⇒a=3×53×45=49ms−2
Now let the mass of A isM . So we can write its equation of motion of A as
Mg−Fcos370=Ma
Putting the values of all the quantities we get
M×10−5×54=M×49⇒M(10−49)=4⇒M=3116kg
So, the force exerted by B on A is 5N and the mass of A is 3116kg .
Therefore, the correct answer is A.
Note:
Here we have to properly analyze the situation and then need to apply the laws of motion. We have to consider certain directions to equate the forces so that we can solve the problem easily. In this problem we first need to determine the acceleration of A and then only we can determine its mass.
