Question
Question: Find force in Newton which mass A exerts on mass B if B is moving forward right with \[3m/{{s}^{2}}\...
Find force in Newton which mass A exerts on mass B if B is moving forward right with 3m/s2. Also find mass A (All surfaces are smooth g=10m/s2)
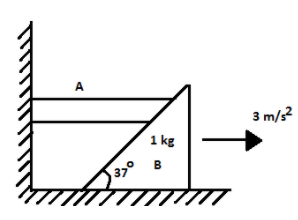
Solution
Given that, mass B is moving with an acceleration due to the force exerted by the mass A. Draw the free body diagram of mass A and mass B. From this, we will get an idea about the forces acting on each body and we can find out the force exerted by mass A on B. To find the mass of A, first we need to calculate the acceleration of A. Then, by balancing the forces in vertical direction, we can calculate the mass.
Complete answer:
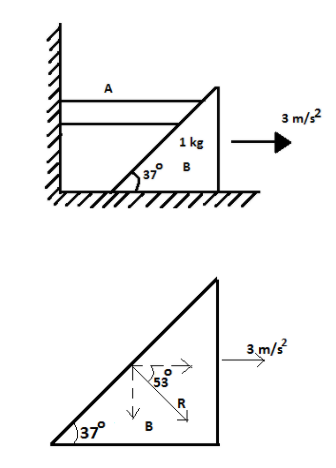
Free body diagram of mass B.
Here, mass B is moving with 3m/s2 acceleration towards right. And the mass A is exerting a normal force R on B. Then, splitting the normal force in to its horizontal and vertical components, we get,
Rcos53=m×a
Substituting the values in above equation, we get,
Rcos53=1×3=3
R×53=3
R=5N
Force exerted by mass A exerts on mass B is 5N,
Now, let’s draw the vector diagram of acceleration of mass A and B.
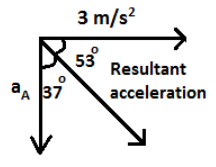
Here, mass B is moving with 3m/s2 acceleration towards right and mass A can only move in the downwards.
Let, the mass A is moving with an acceleration aA.
The resultant acceleration of aA and 3m/s2 is,
aAcos37=3cos53
aA×54=3×53=49m/s2
Acceleration of mass A,aA=49m/s2
Now, let’s draw the free body diagram of A.
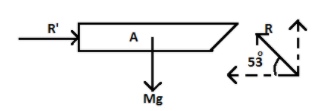
The mass A will experience a reaction force R′ from the wall, and its weight is acting downwards mg. Also, it experiences the reaction force from mass B.
Balancing the forces along the vertical direction we get,
Mg−Rsin53=M×aA
Where, Mis the mass of A.
Substituting the values of g and aA, we get,
M×10−5×54=M×49
Then,
M=3116kg
Mass of A is 3116kg
Therefore, the answer is option A.
Note:
Forces always come in pairs and these pairs are known as action-reaction forces. Identifying the action- reaction force pairs is a simple matter of identifying the two interacting bodies and explaining who is pushing on whom and in what direction. These two forces act against each other, which is explained by Newton’s third law.
