Question

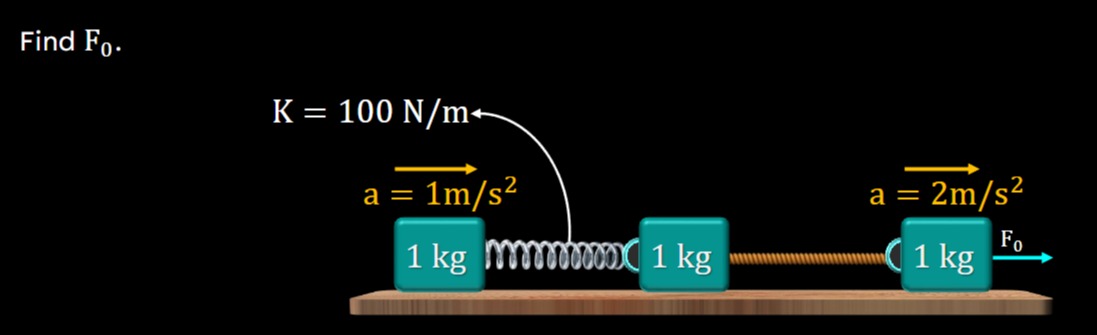
Find $F_0$.

$K=100 N/m \leftarrow$

$a=1m/s^2$ $a=2m/s^2$ $1 kg mmmmmmm 1 kg$ $1kg F_0$

Answer 1

5 N

Answer 2

The system consists of three blocks of mass $m_1=1 \, kg$, $m_2=1 \, kg$, and $m_3=1 \, kg$. The leftmost block is connected to a spring with spring constant $K=100 \, N/m$. The spring is connected to the second block. The second block is connected to the third block by a rod. A force $F_0$ is applied to the rightmost block. The acceleration of the first block is $a_1 = 1 \, m/s^2$ to the right, and the acceleration of the third block is $a_3 = 2 \, m/s^2$ to the right. We need to find $F_0$.

Let $x$ be the compression of the spring from its natural length. A positive $x$ means compression. The force exerted by the spring on the first block is $Kx$ to the right, and on the second block is $Kx$ to the left. Applying Newton's second law to the first block: $Kx = m_1 a_1$ $100x = 1 \times 1 = 1$ $x = 1/100 = 0.01 \, m$. So the spring is compressed by $0.01 \, m$.

Let $T$ be the force exerted by the rod connecting the second and third block on the second block. This force is to the right. By Newton's third law, the force exerted by the second block on the third block is $T$ to the left. Let $a_2$ be the acceleration of the second block to the right. Applying Newton's second law to the second block: $T - Kx = m_2 a_2$ $T - 100(0.01) = 1 \times a_2$ $T - 1 = a_2$

Applying Newton's second law to the third block: $F_0 - T = m_3 a_3$ $F_0 - T = 1 \times 2 = 2$

We have two equations:

1. $T - 1 = a_2$
2. $F_0 - T = 2$

We need to find $F_0$. We need to find $T$ or $a_2$. The problem does not directly provide $a_2$. However, the connection between the second and third block is shown as a rod. A rod is a rigid connection and can transmit both pulling and pushing forces. If the connection is rigid, then the relative acceleration between the two ends of the rod is zero, which means $a_2 = a_3$. Assuming the connection between the second and third block is a rigid rod, then $a_2 = a_3 = 2 \, m/s^2$.

Substitute $a_2 = 2$ into the equation for the second block: $T - 1 = 2$ $T = 3 \, N$.

Now substitute the value of $T$ into the equation for the third block: $F_0 - 3 = 2$ $F_0 = 2 + 3 = 5 \, N$.

Let's check if this is consistent. If $a_2 = 2 \, m/s^2$, $a_1 = 1 \, m/s^2$. The relative acceleration $a_2 - a_1 = 2 - 1 = 1 \, m/s^2$. The compression of the spring is $x = 0.01 \, m$. The force from the spring on the first block is $Kx = 100 \times 0.01 = 1 \, N$, which gives $m_1 a_1 = 1 \times 1 = 1 \, N$. This is consistent. The force from the spring on the second block is $Kx = 1 \, N$ to the left. The force from the rod on the second block is $T = 3 \, N$ to the right. The net force on the second block is $T - Kx = 3 - 1 = 2 \, N$. The mass of the second block is $m_2 = 1 \, kg$, so its acceleration is $a_2 = (T - Kx) / m_2 = 2 / 1 = 2 \, m/s^2$. This is consistent with the assumption $a_2 = a_3 = 2$. The force from the rod on the third block is $T = 3 \, N$ to the left. The applied force is $F_0 = 5 \, N$ to the right. The net force on the third block is $F_0 - T = 5 - 3 = 2 \, N$. The mass of the third block is $m_3 = 1 \, kg$, so its acceleration is $a_3 = (F_0 - T) / m_3 = 2 / 1 = 2 \, m/s^2$. This is consistent with the given $a_3 = 2 \, m/s^2$.

Thus, assuming the connection between the second and third block is rigid, the value of $F_0$ is $5 \, N$.