Question
Question: Find equivalent capacitance between points A and B: [Assume each conducting plate is having same d...
Find equivalent capacitance between points A and B:
[Assume each conducting plate is having same dimensions and neglect the thickness of the plate, dϵ0A=7μF, where A is area of plates]
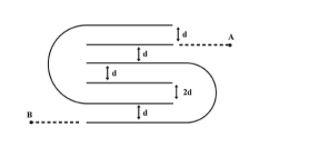
A.7μF
B.11μF
C.12μF
D.15μF
Solution
Draw equivalent circuit of the given circuit. Then calculate equivalent capacitance for the combination. And then using that effective combination find equivalent capacitance between points A and B.
Formula used:
Ceq=C+C+2CC(2C)
CAB=C+Ceq+CCeqC
Complete step-by-step answer:
Given: C=dϵ0A=7μF
Equivalent circuit of the given circuit can be drawn as:
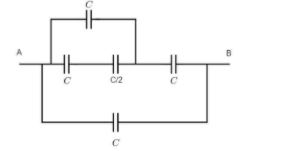
Equivalent capacitance for the combination can be calculated by,
Ceq=C+C+2CC(2C)
∴Ceq=C+3C
∴Ceq=34C
Now by substituting value of C we get,
Ceq=328
Now, equivalent capacitance between points A and B can be given by,
CAB=C+Ceq+CCeqC
Now, substituting the values in above equation we get,
CAB=7+328+7328×7
∴CAB=7+4
∴CAB=11μF
Therefore, the equivalent capacitance between points A and B is 11 μF .
So, the correct answer is “Option B”.
Note: Draw equivalent circuit for every circuit you get. The equivalent circuit makes calculation much easier. Remember the formula to find equivalent connections in series and parallel are different. Such as equivalent series combination for capacitors and resistors is Ceq1=C11+C21+...+CN1 and
Req=R1+R2+...+RN respectively. Vice-versa is the case for equivalent parallel connections.
