Question
Question: Find electric field due to uniformly charged hemispherical cap having charge density $\sigma$ at poi...
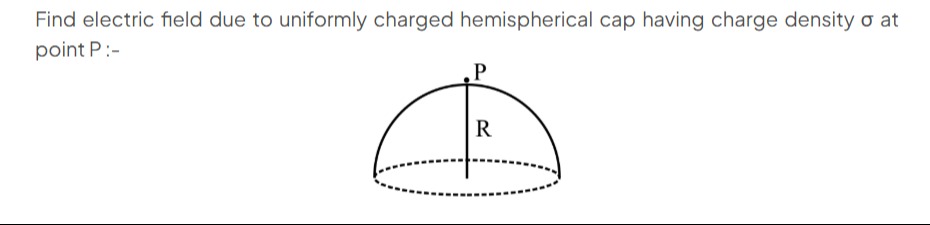
Find electric field due to uniformly charged hemispherical cap having charge density σ at point P :-
E=4ϵ0σz^
Solution
We wish to find the electric field at point P (the top of the hemispherical cap) due to a uniformly charged hemispherical cap of radius R and surface charge density σ.
-
Setup:
Use spherical coordinates where a point on the cap is given by (R,θ,ϕ) with:- θ from 0 to π/2 (since the cap is a hemisphere)
- ϕ from 0 to 2π
-
Choosing an Element of Charge:
dA=R2sinθdθdϕ.
The surface element isIts charge is
dq=σdA=σR2sinθdθdϕ. -
Contribution to the Electric Field:
dE=4πϵ01R2dqr^,
The field from dq at P (which is on the axis through the center of curvature) is given by Coulomb's law:where the distance from each element to point P is R (due to the symmetry of the spherical surface) and r^ will have a component along the vertical (z-) direction given by cosθ. Hence, the vertical component is
dEz=4πϵ01R2σR2sinθdθdϕcosθ=4πϵ0σsinθcosθdθdϕ. -
Integrating:
Ez=4πϵ0σ∫ϕ=02πdϕ∫θ=0π/2sinθcosθdθ.
Integrate over the entire cap:The ϕ-integral gives:
∫02πdϕ=2π.The θ-integral:
∫0π/2sinθcosθdθ.Use the substitution u=sinθ so du=cosθdθ. When θ=0, u=0; when θ=π/2, u=1. Thus,
∫01udu=21.Putting it together:
Ez=4πϵ0σ(2π)(21)=4ϵ0σ. -
Result:
E=4ϵ0σz^.
The net electric field at P is:
