Question

Find effective resistance between A and B.

A.$\dfrac{5}{7}\Omega$
B. $7\Omega$
C.$\dfrac{8}{7}\Omega$
D. $9\Omega$

Answer 1

Hint: In the given combination, you could look for point of symmetry such that we could detach the connection there without affecting the effective resistance of the combination. Then you could look for series and parallel connections and solve it part by part and the end you will get the required effective resistance.
Formula used:
Expression for resistance of:
Series combination,
${{R}_{eff}}={{R}_{1}}+{{R}_{2}}$
Parallel combination,
$\dfrac{1}{{{R}_{eff}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}$

Complete Step by step solution:
In the question, we are given a combination of 7 resistors and we are asked to find the effective resistance across points A and B.
An important point to be remembered here is that when there exists symmetry about a particular point, detaching the connection from there doesn’t affect the effective resistance. To make the point clear we could use the given combination of resistors.

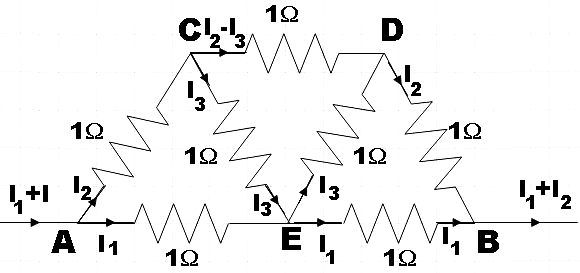
We see that the given combination has symmetry at point E. So, we could detach CED from AEB without affecting the effective resistance as the current flowing in the arm CE and arm ED is also the same.

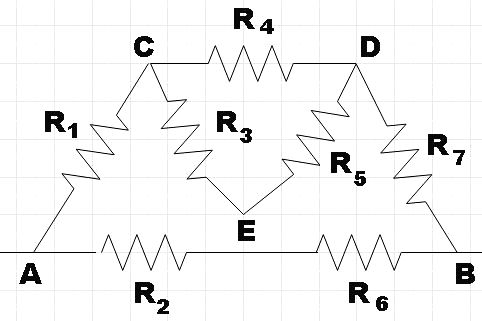
Now let us recall the expressions for resistance of:
Series combination,
${{R}_{eff}}={{R}_{1}}+{{R}_{2}}$
Parallel combination,
$\dfrac{1}{{{R}_{eff}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}$
Now, along CED we have two resistors ${{R}_{3}}$ and ${{R}_{5}}$ connected in series,
${{R}_{35}}={{R}_{3}}+{{R}_{5}}$
$\Rightarrow {{R}_{35}}=1\Omega +1\Omega =2\Omega$
But ${{R}_{35}}$ is parallel to${{R}_{4}}$,
${{R}_{CD}}=\dfrac{{{R}_{35}}\times {{R}_{4}}}{{{R}_{35}}+{{R}_{4}}}$
$\Rightarrow {{R}_{CD}}=\dfrac{2\times 1}{2+1}=\dfrac{2}{3}$
But we see that ${{R}_{CD}}$ is in series with ${{R}_{1}}$ and${{R}_{7}}$,
${{R}_{ACDB}}=\left( 1+\dfrac{2}{3}+1 \right)\Omega$
$\Rightarrow {{R}_{ACDB}}=\dfrac{8}{3}\Omega$ ……………………………….. (1)
Now, we have ${{R}_{2}}$ and${{R}_{6}}$ which are connected in series,
${{R}_{26}}=\left( 1+1 \right)\Omega$
$\Rightarrow {{R}_{26}}=2\Omega$ ……………………………………………. (2)
Also, we see that ${{R}_{ACDB}}$ and ${{R}_{26}}$ are parallel to each other, so,
${{R}_{AB}}=\dfrac{{{R}_{ACDB}}\times {{R}_{26}}}{{{R}_{ACDB}}+{{R}_{26}}}$
Substituting (1) and (2), we have,
$\Rightarrow {{R}_{AB}}=\dfrac{\dfrac{8}{3}\times 2}{\dfrac{8}{3}+2}$
$\Rightarrow {{R}_{AB}}=\dfrac{\dfrac{16}{3}}{\dfrac{14}{3}}=\dfrac{16}{14}$
$\therefore {{R}_{AB}}=\dfrac{8}{7}\Omega$
Therefore, we found the effective resistance across A and B to be,
${{R}_{AB}}=\dfrac{8}{7}\Omega$

Hence, option C is found to be the answer.

Note:
For questions where we are asked to find the effective resistance, you can firstly simplify the complex combination into simple series and parallel connections. Sometimes, you may find other simplifications where we have a Wheatstone bridge in the combination. We could then find the effective resistance for simple series and parallel connections and hence the effective resistance of the combination.