Question

Find DRG of $f(x) = 2024 + \sqrt{2x - 1 + 2\sqrt{x^2 - x}} \;-\; \sqrt{x - 1}$

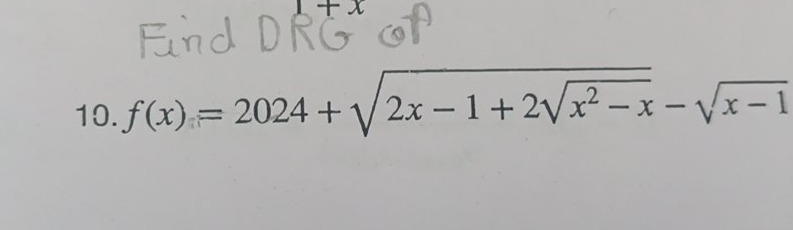
Answer 1

$x \ge 1$

Answer 2

Step 1. Under the first radical:

$$2x - 1 + 2\sqrt{x^2 - x} = (\sqrt{x} + \sqrt{x - 1})^2,$$

valid for $x\ge1$.

Step 2. Thus

$$\sqrt{2x - 1 + 2\sqrt{x^2 - x}} = \sqrt{(\sqrt{x} + \sqrt{x - 1})^2} = \sqrt{x} + \sqrt{x - 1}.$$

Step 3. Substituting back,

$$f(x) = 2024 + (\sqrt{x} + \sqrt{x - 1}) - \sqrt{x - 1} = 2024 + \sqrt{x}.$$

Domain condition:
Both $\sqrt{x - 1}$ and $\sqrt{x}$ require $x \ge 1$.
Therefore, the domain (DRG) is

$$\boxed{x \ge 1}.$$