Question
Question: Find by integration, the area bounded by the curve \(y=2x-{{x}^{2}}\) and the x-axis....
Find by integration, the area bounded by the curve y=2x−x2 and the x-axis.
Solution
Hint: Plot the curve on a graph. Use the fact that the area bounded by the curve y = f(x), the x-axis, and the ordinates x= a and x = b is given by ∫ab∣f(x)∣dx. Argue that the required area is the area bounded by the curve y=2x−x2, the x-axis and the ordinates x= 0 and x= 2.Hence prove that the required area is ∫02(2x−x2)dx. Integrate and hence find the required area.
Complete step-by-step answer:
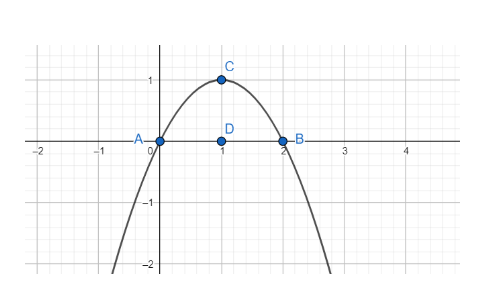
As is evident from the graph, the area bound the curve y=2x−x2 is equal to the area ACBDA.
Finding the coordinates of A and B:
As is evident from the A and B are the roots of f(x)=2x−x2
Hence, we have
2x−x2=0⇒x=0,2
Hence, we have A≡(0,0) and B≡(2,0)
Hence the area ACBDA is the area bounded by the curve y=2x−x2, the x-axis and the ordinates x= 0 and x= 2.
We know that the area bounded by the curve y = f(x), the x-axis, and the ordinates x= a and x = b is given by ∫ab∣f(x)∣dx
Hence, we have
Required area =∫022x−x2dx
Now, we have 2x−x2=x(2−x)
In the interval (0,2), we have x and 2-x both are non-negative
Hence, we have x(2−x)≥0
Hence, we have
∣x(2−x)∣=x(2−x)
Hence, we have
Required area =∫02(2x−x2)dx=x2−3x302=(4−38)=34 square units.
Note: Alternative use the fact that the area bounded by the curve y=C(x−a)(x−b) and the x-axis is given by 6∣C∣(a−b)3
Here, we have 2x−x2=−(x−0)(x−2)
Hence a = 0, b = 2 and C =-1
Hence the required area is 6∣−1∣(2−0)3=68=34, which is the same as obtained above.
