Question
Question: Find by integration the area bounded by the curve \({{y}^{2}}=4ax\) and the lines y = 2a and x=0....
Find by integration the area bounded by the curve y2=4ax and the lines y = 2a and x=0.
Solution
Hint: Plot the curve on the graph paper. Identify the region whose area is to be found. Argue that the area of the region is equal to the difference between the area bounded by the curve y=2a, the x-axis and the ordinates x= 0 and x= a and the area bounded by the curve y=2ax, the x-axis and the ordinates x=0 and x=a. Use the fact that the area bounded by the curve y=f(x), the x-axis and the ordinates x=a and x= b is given by A=∫ab∣f(x)∣dx. Hence determine the individual areas and hence the total area.
Complete step-by-step answer:
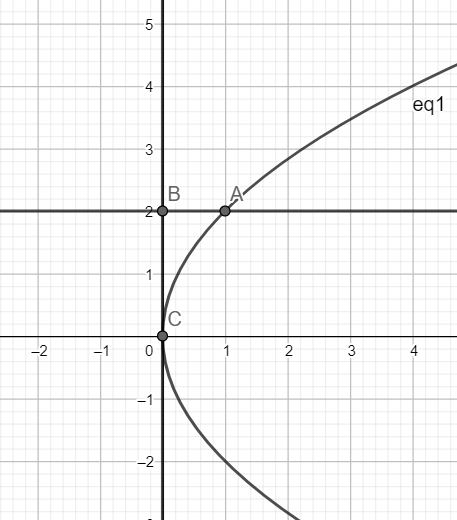
The region whose area is to be found is ABCA.
Finding the coordinates of point A:
We have A is the point of intersection of y = 2a and y2=4ax
Hence, we have 4x=2a2=4a2⇒x=a
Hence, we have A≡(a,2a)
The arm AC of the parabola y2=4ax has y≥0
Hence for the arm AC of the parabola, the equation is y=2ax
As is evident from the graph, the area of the region to be found is the difference between the area bounded by the curve y=2a, the x-axis and the ordinates x= 0 and x= a and the area bounded by the curve y=2ax, the x-axis and the ordinates x=0 and x=1.
Now, we know that the area of the region bounded by the curve y=f(x), the x-axis and the ordinates x=a and x= b is given by A=∫ab∣f(x)∣dx.
Hence the area of the region bounded by the curve y = 2a, the x-axis and the ordinates x=0 and x=a is given by A1=∫0a2adx=2a2
Also, the area of the region bounded by the curve y=2ax, the x-axis and the ordinates x= 0 and x= a is given by A2=∫0a2axdx=
We know that ∫xndx=n+1xn+1+C
Hence, we have
A2=2a32x230a=34a2
Hence the required area is given by A=A1−A2=2a2−34a2=32a2
Hence the required area is 32a2 square units.
Note: We can also take horizontal strips to find the area as shown below
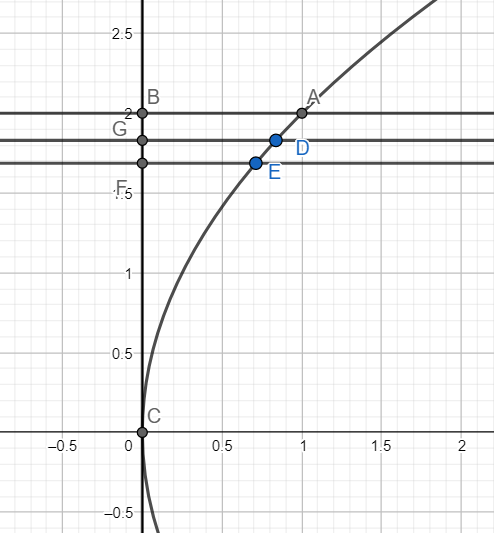
For the strip DEFG, we have GD =x=4ay2 and GF = dy
Hence the area of the region =∫02a4ay2dy=12ay302a=32a2, which is the same as obtained above.
