Question
Question: Find area enclosed by $y = ex. lnx, y = \frac{ln x}{ex}$....
Find area enclosed by y=ex.lnx,y=exlnx.
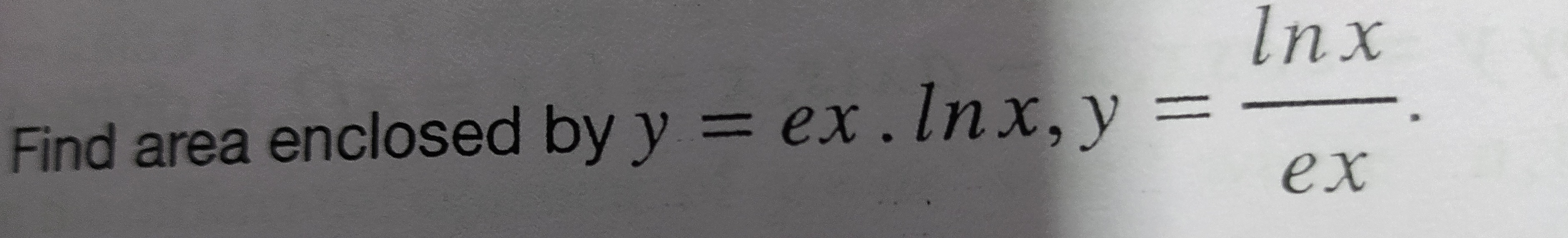
4ee2−5
Solution
To find the area enclosed by the two curves y=exlnx and y=exlnx, we first need to find their points of intersection.
1. Find the Intersection Points: Set the two equations equal to each other: exlnx=exlnx Multiply both sides by ex (assuming x=0): e2x2lnx=lnx e2x2lnx−lnx=0 lnx(e2x2−1)=0
This equation gives two possibilities:
- lnx=0⟹x=e0=1.
- e2x2−1=0⟹e2x2=1⟹x2=e21⟹x=±e1. Since lnx is defined only for x>0, we take x=e1.
So, the intersection points are x=e1 and x=1.
2. Determine Which Curve is Above the Other: Let f(x)=exlnx and g(x)=exlnx. We need to determine which function is greater in the interval (e1,1). Consider the difference g(x)−f(x): g(x)−f(x)=exlnx−exlnx=lnx(ex1−ex)=lnx(ex1−e2x2).
In the interval x∈(e1,1):
- lnx is negative (since x<1).
- Since x>e1, we have x2>e21, which implies e2x2>1. Therefore, 1−e2x2 is negative.
- ex is positive.
So, the term lnx(ex1−e2x2) is (negative) × (negative) × (positive) = positive. This means g(x)−f(x)>0, so g(x) is the upper curve and f(x) is the lower curve in the interval (e1,1).
3. Set up the Definite Integral for the Area: The area A enclosed by the curves is given by: A=∫1/e1(g(x)−f(x))dx=∫1/e1(exlnx−exlnx)dx
4. Evaluate the Integral: We integrate term by term.
-
Integral of the first term: ∫exlnxdx=e1∫xlnxdx. Let u=lnx, then du=x1dx. e1∫udu=e12u2=2e(lnx)2.
-
Integral of the second term: ∫exlnxdx. Use integration by parts: ∫PQ′dx=PQ−∫P′Qdx. Let P=lnx and Q′=ex. Then P′=x1 and Q=2ex2. ∫exlnxdx=(lnx)(2ex2)−∫(x1)(2ex2)dx =2ex2lnx−∫2exdx =2ex2lnx−4ex2.
Now, combine these results to find the indefinite integral of g(x)−f(x): ∫(exlnx−exlnx)dx=2e(lnx)2−(2ex2lnx−4ex2) =2e(lnx)2−2ex2lnx+4ex2.
Now, evaluate this definite integral from x=e1 to x=1: A=[2e(lnx)2−2ex2lnx+4ex2]1/e1
-
At the upper limit x=1: 2e(ln1)2−2e(1)2ln1+4e(1)2=2e0−2e⋅0+4e=4e.
-
At the lower limit x=e1: Note that ln(e1)=ln(e−1)=−1. 2e(ln(e1))2−2e(e1)2ln(e1)+4e(e1)2 =2e(−1)2−2e⋅e21⋅(−1)+4e⋅e21 =2e1−2e1⋅(−1)+4e1 =2e1+2e1+4e1 =2e2+4e1=e1+4e1=4e4+1=4e5.
Finally, subtract the value at the lower limit from the value at the upper limit: A=4e−4e5=4ee2−4e5=4ee2−5.
The area enclosed by the curves is 4ee2−5.
