Question

Find area enclosed by $(y - sin^{-1}x)^2 = x - x^2$.

Answer 1

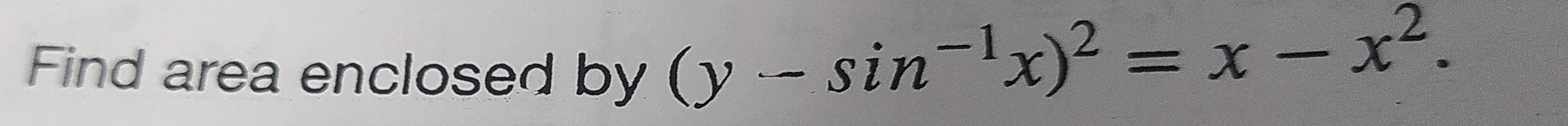
The area enclosed by the curve is $\frac{\pi}{4}$.

Answer 2

The given equation is $(y - \sin^{-1}x)^2 = x - x^2$.

Step 1: Determine the domain for x. For the right-hand side, $x - x^2$, to be defined and non-negative (since it's equal to a square), we must have: $x - x^2 \ge 0$ $x(1 - x) \ge 0$ This inequality holds true for $0 \le x \le 1$. Additionally, for $\sin^{-1}x$ to be defined, $x$ must be in the interval $[-1, 1]$. Combining these conditions, the valid domain for $x$ is $[0, 1]$.

Step 2: Express y in terms of x. Taking the square root of both sides of the given equation: $y - \sin^{-1}x = \pm\sqrt{x - x^2}$ This gives two functions for $y$:

1. $y_1 = \sin^{-1}x + \sqrt{x - x^2}$
2. $y_2 = \sin^{-1}x - \sqrt{x - x^2}$

Step 3: Set up the integral for the area. The area enclosed by the curve is the area between the two functions $y_1$ and $y_2$ over the interval $[0, 1]$. Area $A = \int_{0}^{1} (y_1 - y_2) dx$ $A = \int_{0}^{1} \left[ (\sin^{-1}x + \sqrt{x - x^2}) - (\sin^{-1}x - \sqrt{x - x^2}) \right] dx$ $A = \int_{0}^{1} 2\sqrt{x - x^2} dx$

Step 4: Simplify the integrand by completing the square. The term inside the square root, $x - x^2$, can be rewritten by completing the square: $x - x^2 = -(x^2 - x) = -\left(x^2 - x + \frac{1}{4} - \frac{1}{4}\right) = -\left(\left(x - \frac{1}{2}\right)^2 - \frac{1}{4}\right) = \frac{1}{4} - \left(x - \frac{1}{2}\right)^2$

Now, the integral becomes: $A = 2 \int_{0}^{1} \sqrt{\frac{1}{4} - \left(x - \frac{1}{2}\right)^2} dx$

Step 5: Evaluate the integral using a substitution or geometric interpretation. Let $u = x - \frac{1}{2}$. Then $du = dx$. When $x = 0$, $u = 0 - \frac{1}{2} = -\frac{1}{2}$. When $x = 1$, $u = 1 - \frac{1}{2} = \frac{1}{2}$. The integral transforms to: $A = 2 \int_{-1/2}^{1/2} \sqrt{\left(\frac{1}{2}\right)^2 - u^2} du$

The integral $\int_{-a}^{a} \sqrt{a^2 - u^2} du$ represents the area of a semicircle with radius $a$. In this case, $a = \frac{1}{2}$. The area of a semicircle with radius $a$ is $\frac{1}{2}\pi a^2$. So, $\int_{-1/2}^{1/2} \sqrt{\left(\frac{1}{2}\right)^2 - u^2} du = \frac{1}{2}\pi \left(\frac{1}{2}\right)^2 = \frac{1}{2}\pi \left(\frac{1}{4}\right) = \frac{\pi}{8}$.

Therefore, the total area $A$ is: $A = 2 \times \frac{\pi}{8} = \frac{\pi}{4}$