Question

Find an expression for the maximum permissible velocity of a car moving along a banked road. If the coefficient of the static friction between the tyres and road is ${{\mu }_{s}}$.

Answer 1

As a first step make a neat diagram of the situation by marking all the forces that are acting on the car on a banked road. Now resolve the components accordingly and balance the forces along vertical and horizontal directions. Now divide these two equations and then rearrange to get the required maximum permissible velocity.

Formula used:
Expression for centripetal force,
${{F}_{C}}=\dfrac{m{{v}^{2}}}{r}$

Complete step by step answer:
Let us recall that banking on the road is done so as to avoid skidding while taking turns around the road. It has another advantage that it reduces the wear and tear of car tyres. By banking of roads we mean that the road surface at a bend is slightly tilted inwards, that is, the outer edge of the road is raised above the inner side. In the question we are asked to find the expression for maximum permissible velocity of a car moving along a banked road. Consider a car of mass m that is taking a right turn on a road of radius r that is banked at an angle$\theta$. The banking is done such that the road will have an optimum speed v.

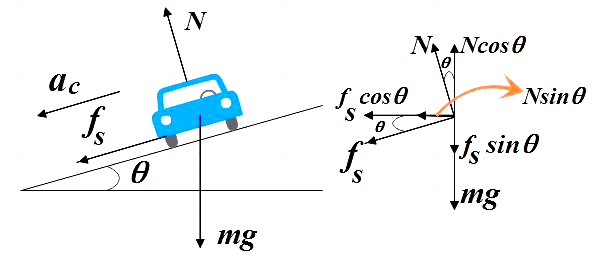
We have weight of the body acting vertically downwards, normal reaction of road that is perpendicular to road surface and frictional force along the inclined road. Now on resolving the frictional force and normal reaction we get ${{f}_{s}}\cos \theta$ and $N\sin \theta$ acting horizontal towards the centre of the circular path and $N\cos \theta$ acting vertically upward and ${{f}_{s}}\sin \theta$ acting vertically downward.
Also, we know that there is centripetal force acting on the car towards the centre of the circular path. For maximum velocity${{v}_{\max }}$ let us balance all the above given forces.
Horizontally we have,
$\dfrac{m{{v}_{\max }}^{2}}{r}=N\sin \theta +{{f}_{s}}\cos \theta$
$\Rightarrow \dfrac{m{{v}_{\max }}^{2}}{r}=N\sin \theta +{{\mu }_{s}}N\cos \theta =N\left( \sin \theta +{{\mu }_{s}}\cos \theta \right)$ ……………………… (1)
Vertically we have,
$N\cos \theta =mg+{{f}_{s}}\sin \theta$
$\Rightarrow mg=N\cos \theta -{{\mu }_{s}}N\sin \theta =N\left( \cos \theta -{{\mu }_{s}}\sin \theta \right)$ …………………………….. (2)
Dividing (1) by (2),
$\dfrac{m{{v}_{\max }}^{2}}{rmg}=\dfrac{N\left( \sin \theta +{{\mu }_{s}}\cos \theta \right)}{N\left( \cos \theta -{{\mu }_{s}}\sin \theta \right)}$
$\Rightarrow \dfrac{{{v}_{\max }}^{2}}{rg}=\dfrac{\sin \theta +{{\mu }_{s}}\cos \theta }{\cos \theta -{{\mu }_{s}}\sin \theta }$
Dividing the numerator and denominator on the RHS by$\cos \theta$, we get,
$\dfrac{{{v}_{\max }}^{2}}{rg}=\dfrac{\tan \theta +{{\mu }_{s}}}{1-{{\mu }_{s}}\tan \theta }$
$\Rightarrow {{v}_{\max }}=\sqrt{\dfrac{rg\left( \tan \theta +{{\mu }_{s}} \right)}{1-{{\mu }_{s}}\tan \theta }}$
Hence, we get the expression for the maximum permissible velocity of a car moving along a banked road with coefficient of the static friction between the tyres and road as ${{\mu }_{s}}$ is ${{v}_{\max }}=\sqrt{\dfrac{rg\left( \tan \theta +{{\mu }_{s}} \right)}{1-{{\mu }_{s}}\tan \theta }}$

Note:
We could also find the optimum speed on this circular banked road. At optimum speed the friction between car tyres and surface of road is negligible, so${{\mu }_{s}}=0$, optimum speed v is given by,
$v=\sqrt{rg\tan \theta }$
There we get the angle of banking as,
$\theta ={{\tan }^{-1}}\left( \dfrac{{{v}^{2}}}{rg} \right)$
We see that the angle of banking is independent of the mass of the vehicle.