Question
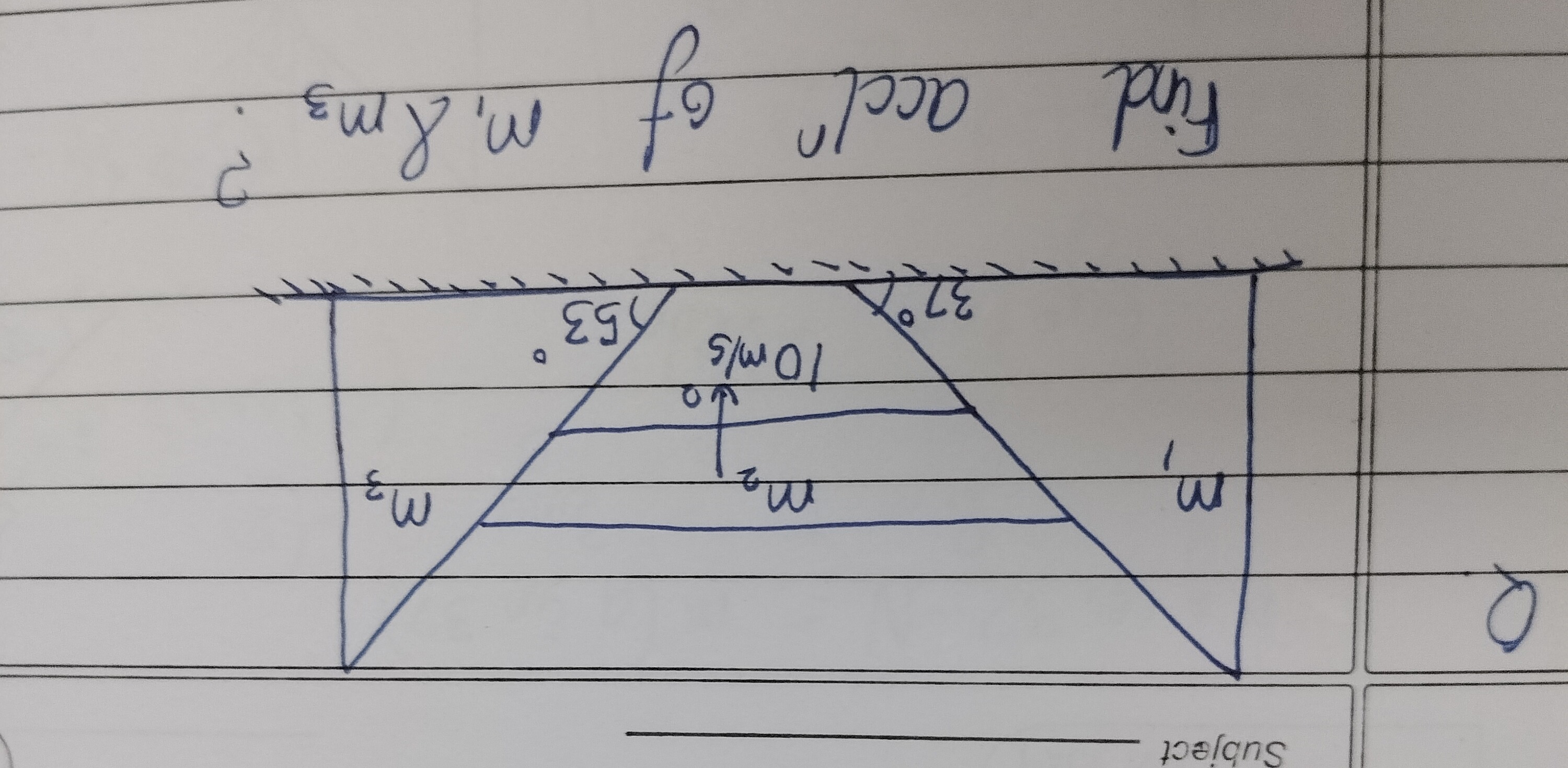
Question: Find accl of $m_1 \& m_3$?...
Find accl of m1&m3?
The acceleration of m1 is 9m/s2 down the 53∘ incline, and the acceleration of m3 is 11m/s2 down the 37∘ incline.
Solution
The problem describes a pulley system with three masses: m1 on a 53∘ incline, m3 on a 37∘ incline, and m2 accelerating upwards at 10m/s2.
A common constraint relation for such pulley systems is a1+a3=2a2, where a1 and a3 are accelerations down their respective inclines, and a2 is the upward acceleration of m2.
Given a2=10m/s2, we have a1+a3=2×10m/s2=20m/s2.
Assuming m1=m3=m (a common implication in such problems when masses are not specified) and T is the tension in the string, we apply Newton's second law along the inclined planes:
For m1: T−mgsin(53∘)=ma1 For m3: T−mgsin(37∘)=ma3
Subtracting the second equation from the first: mg(sin(37∘)−sin(53∘))=m(a1−a3) g(sin(37∘)−sin(53∘))=a1−a3
Using approximations: g≈10m/s2, sin(53∘)≈0.8, sin(37∘)≈0.6. 10(0.6−0.8)=a1−a3 −2=a1−a3
We now have a system of linear equations:
- a1+a3=20
- a1−a3=−2
Adding (1) and (2): 2a1=18⟹a1=9m/s2 (downwards along 53∘ incline)
Substituting a1 into (1): 9+a3=20⟹a3=11m/s2 (downwards along 37∘ incline)
Therefore, the acceleration of m1 is 9m/s2 and the acceleration of m3 is 11m/s2.
