Question
Question: Find acceleration, normal reaction and tension in each case. \(\left( {g = 10\,m/{s^2}} \right)\) ...
Find acceleration, normal reaction and tension in each case. (g=10m/s2)
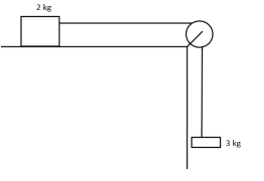
Solution
This question is pretty simple if you know that tension on both parts of the strings is exactly the same around the pulley, since the strings are considered massless, the question gets even simpler. Also, the surfaces are given to be smooth, hence, there is no friction in the given question. All you need to do is to equate the tension and assume the acceleration of the 2kg mass as a which is the acceleration asked in the question.
Complete step by step answer:
We will proceed with the solution exactly as told in the hint section of the solution to the question.
Let us assume a tension T1 in the vertical section of the string.
We’ve been given the mass of the lower block as M1=3kg
Using this, we can say that:
T1=M1g
After substituting in the values, we get:
T1=30N
Now, let’s assume a tension T2 in the horizontal section of the string, since tension in the string around the pulley is always equal, we can say:
T2=T1=30N
Now, let us assume the mass M2=2kg moving with an acceleration of magnitude a, now we can say that:
M2a=T2
We’ve already found out the value of tension in the horizontal section of the string to be the same as the tension in the vertical section of the string. Using this, we can write:
(2)a=30N a=15m/s2
We also need to find the value of normal reaction force on the mass M2(=2kg)
We know that normal force is the force perpendicular to the surface. Since there is no vertical movement of the mass M2, we can safely say that the normal force in this case is equal to the weight of the box. Hence:
N=M2g N=20N
We’ve found out the values of:
Acceleration, a=15m/s2
Normal reaction, N=20N
Tension, T=T1=30N
Note: Many students commit mistakes by adding the two masses and finding the acceleration by dividing the tension with the combined mass. Although both of the boxes move with the same acceleration, you need to know that only the mass M2 is contributing to the value of acceleration.
