Question

Find a way to mathematically find instantaneous velocity from a position versus time graph.

Answer 1

Hint : The instantaneous velocity at any given point $p(x,t)$ on the function $p(x,t)$ in a graph is velocity at a particular instance of time.

Complete step by step solution:
At any given point, the derivative of a function is simply the instantaneous rate of change of the function at that point which means that the derivative at a given point ${p_0}({x_0},{t_0})$ is the instantaneous rate of change in position (accounting for "positive" and "negative" direction) with respect to time in the case of a graph of position (or distance) vs. time.
Consider, as an example, a linear distance function. If this was a function of $x$ and $y$ where the latter one acts as the dependent variable, then our slope-intercept function will take the form of our function
$y = mx + c$
Where $m = {\text{slope}}$ and $c$ stands for the value of $y$ at $x = 0$
Applying this theory to our question we have $t$ as an independent variable and $x$ as the dependent variable. So our linear equation will look like the following function
$x(t) = mt + b$
From algebra, we know that for every single unit of change in the independent variable, the slope of a line calculates the number of units of change in the dependent variable.
So we take a line, say: $x(t) = 7t + 3$ , here for every one unit increase in $t$ our $x$ increases by 7 units. In simpler terms, our distance will increase 7 units for every unit increase in time.
Here is the graphical representation of the expression roughly

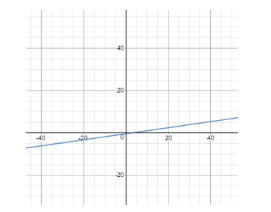
Since our change in distance per unit of time shift will remain the same, in this case, regardless of our starting point $\left( {{x_0},{t_0}} \right)$ we can be certain that our instantaneous velocity is the same.

Note : The case discussed in our answer is only similar to our average velocity of the function by design: this would not be the case for a nonlinear function for example $\left( {x(t) = 2{x^3}} \right)$ , and to find the derivatives of such functions, we would need to use differentiation techniques.