Question
Question: Find a rational number between -1 and 1. A. 0 B. \(\dfrac{1}{\sqrt{-2}}\) C. \(\dfrac{-8}{5}\...
Find a rational number between -1 and 1.
A. 0
B. −21
C. 5−8
D. 23
Solution
Hint: First of all check if a number is rational as not by checking that it should be of the form qp where p and q are integers and q=0.
Complete step-by-step answer:
Then check if that number is between -1 and 1 in the number line.
Here we have to find the rational number between -1 to 1 out of given options.
Before proceeding with the question we must know what a rational number is.
A rational number is a number that can be expressed in the form of qp where p and q are integers and q=0. Since q may be equal to 1, hence every integer is a rational number. Examples are 0,1,2,32,−4,7−6,etc
Now we will see what a number line is. A number line is a straight line with numbers placed at equal intervals or segments along its length. A number line contains all real numbers that are rational numbers and irrational numbers both.
We can show number line as
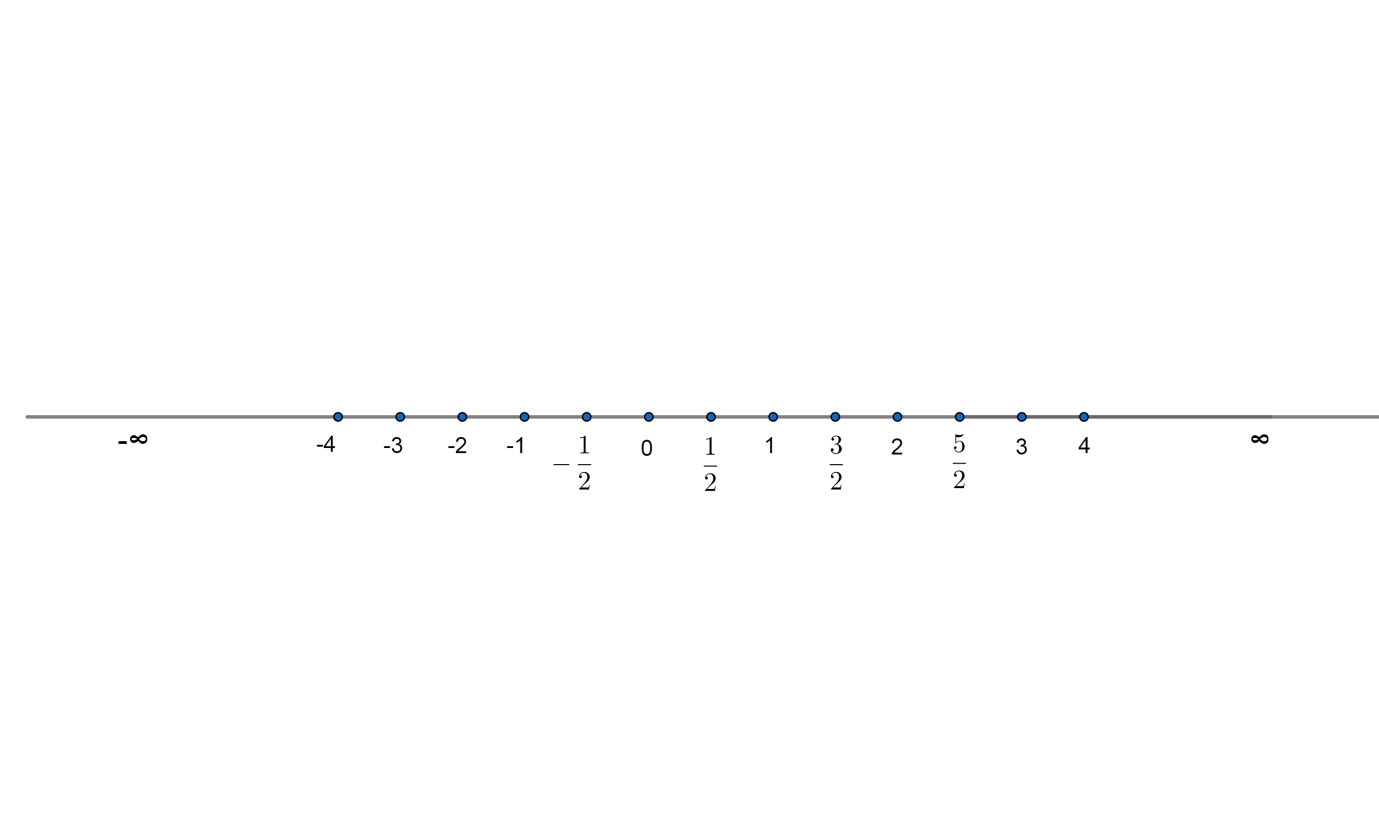
Now we will find the rational number between -1 and 1 out of given options.
(A) 0
Since we know that all integers are rational numbers. Therefore, 0 is also a rational number.
Also we know that 0 lies between -1 and 1 in number line as shown,
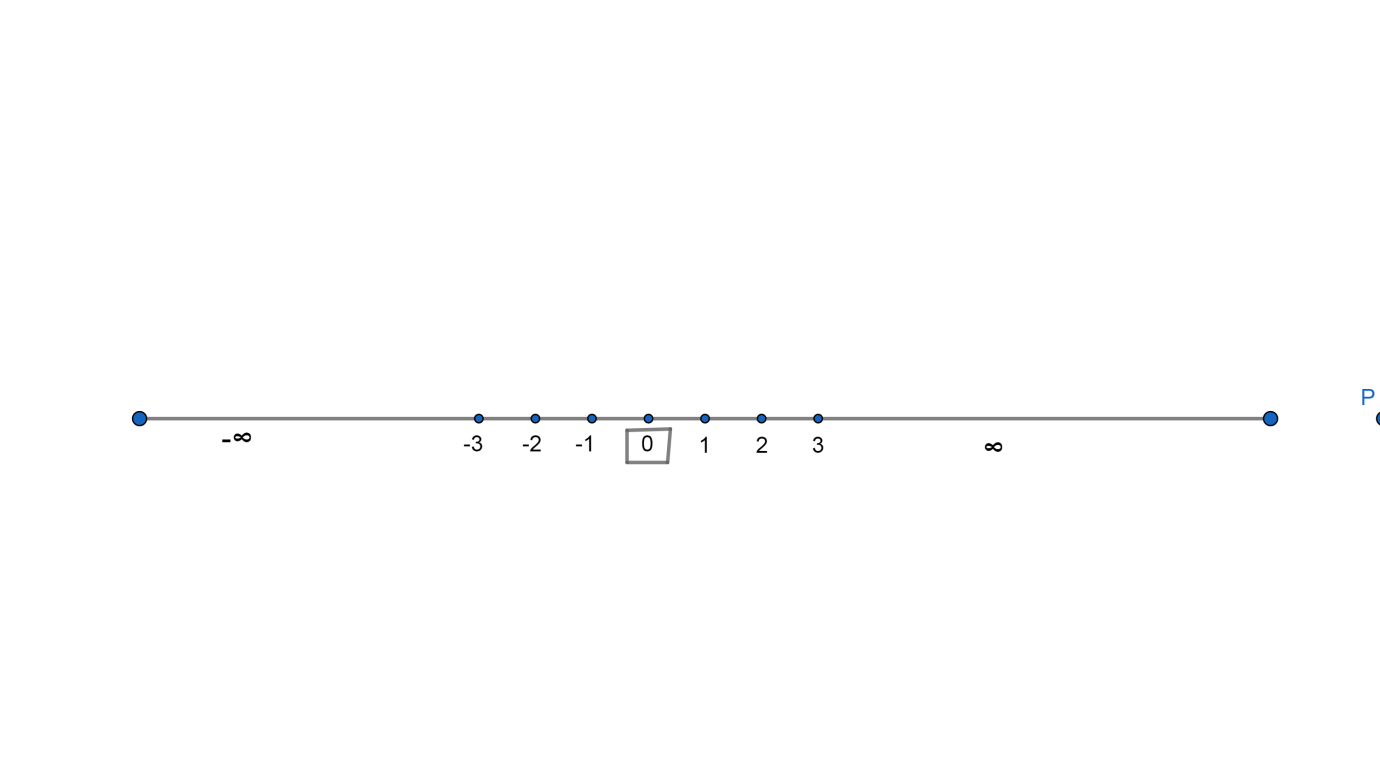
Therefore, we can say that 0 is a rational number between -1 and 1. Therefore, this option is correct.
(B) −21
Since we know that in any rational number of form qp, p and q must be integer but here −2 is not an integer but an imaginary number, so −21is not a rational number. Therefore, this option is incorrect.
(C) 5−8
5−8is a rational number because it is in form of qpthat is 5−8where -8 and 5 are integers.
In decimal form we can write 5−8=−1.6
In number line we can show – 1.6 or 5−8 as
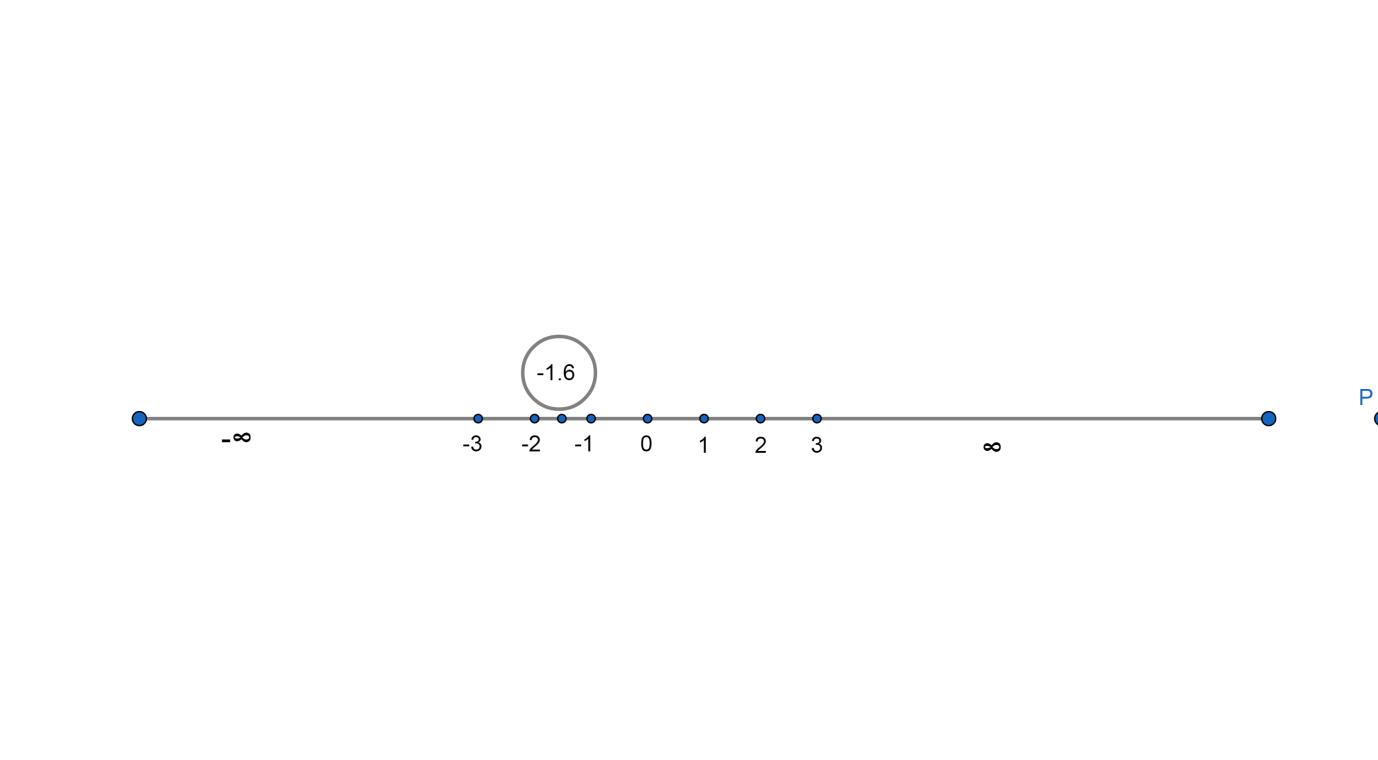
Since – 1.6 or 5−8 does not lie between – 1 and 1. So this option is incorrect.
(D) 23
23is a rational number because it is in form of qp that is 23where 3 and 2 are integers.
In decimal form we can write 23=1.5
In number line, we can show 1.5 or 23 as;
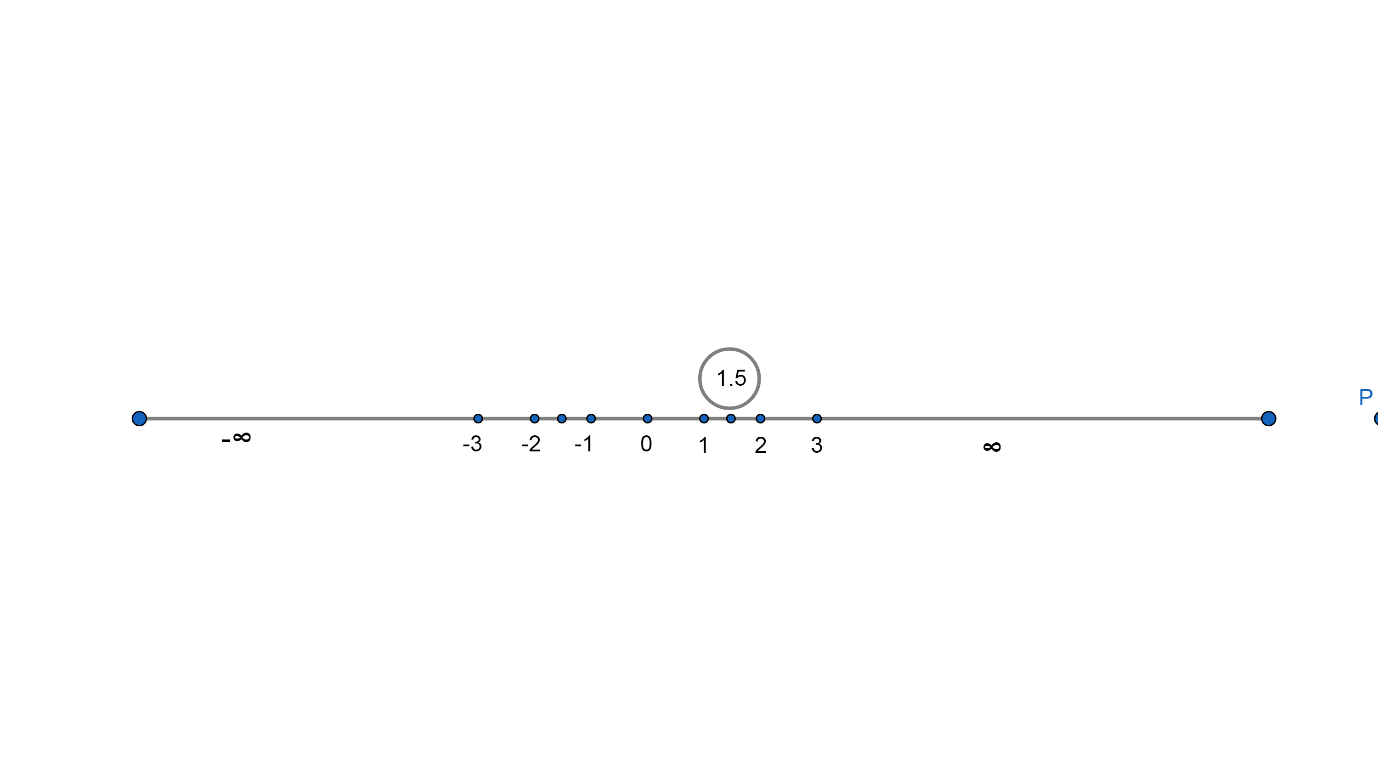
Since, 1.5 or 23does not lie between -1 and 1.
So this option is incorrect.
Hence option (A) is correct.
Note: Students must note that there are infinitely many rational numbers between any two numbers but here we must check from option to get rational numbers -1 and 1. Before checking if a number lies between -1 and 1 or not, students must check if it is rational or not. It is always better to convert fractional form to decimal form to judge the magnitude of a number correctly.
