Question

Fill in the blanks to make each of the following a true statement:
(i) $A \cup A' = ...$
(ii) $\phi ' \cap A = ...$
(iii) $A \cap A' = ...$
(iv) $U' \cap A = ...$

Answer 1

We can break the complex Venn diagrams into easier forms then use them to create the main Venn diagram it will help us understanding the basics also we can use Venn diagrams to easily interpret the left side to get the results to fill in the right sides.

Complete step-by-step answer:
Part No. 1 $A \cup A' = ...$
To get the answer of $A \cup A'$ , we will have to divide it into smaller parts or portions like $A$ and $A'$ .
Now, let’s draw some Venn diagrams of $A$ and $A'$ . Which looks like this.

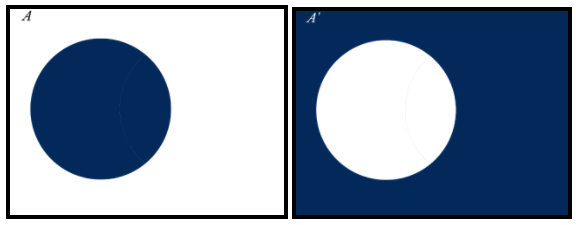
Now we have to take the union of these both diagrams of $A$ and $A'$ , For that we will remove the white part and overlap both of them and we get the final result which is like this.

As, We can see it covers the whole area which is a Universal set.
Hence, We can say it’s a Universal Set
$\therefore A \cup A' = U$
Part No. 2 $\phi ' \cap A = ...$
To get the answer of $\phi ' \cap A$ , we will have to divide it into smaller parts or portions like $\phi '$ and $A$ .
$\phi '$ which is a complement of $\phi$ means an empty set, that means $\phi '$ is a Universal Set.
So, we can rewrite it as $U \cap A$ .
$\therefore \phi ' \cap A = U \cap A$
When we write $U \cap A$ it simply means that we are taking the intersection of $A{\rm{ }}and{\rm{ }}U$ .
$U$ is a universal set and it consists of all the possible sets. Hence taking anything intersection from it would result in the original Set that is $A$ in this case.
$\therefore U \cap A = A$
$\therefore \phi ' \cap A = A$
Part No. 3 $A \cap A' = ...$
To get the answer of $A \cap A'$ , we will have to divide it into smaller parts or portions like $A$ and $A'$ .
Now, let’s draw some Venn diagrams of $A$ and $A'$ . Which looks like this.

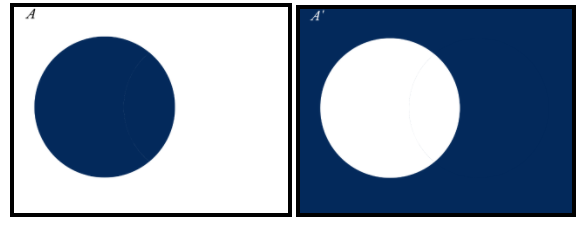
To get the answer of $A \cap A'$ , we will overlap both the Venn Diagrams and see if any area overlaps two times which means that is common in both sets. But here one is complement of the other so after overlapping we don’t see any area which is common in both sets.
Hence, $A \cap A'$ represents a Null Set.
$\therefore A \cap A' = \phi$
Part No. 4 $U' \cap A = ...$
To get the answer of $U' \cap A$ , we will have to divide it into smaller parts or portions like $U'$ and $A$
$U'$ which is a complement of $U$ means an Universal set, that means $U'$ is a Null Set.
So, we can rewrite it as $\phi \cap A$ .
$\therefore U' \cap A = \phi \cap A$
When we write $\phi \cap A$ it simply means that we are taking the intersection of $A{\rm{ }}and{\rm{ }}\phi$ .
$\phi$ is a Null set or we can simply say it is an empty set in layman. Hence taking anything intersection from it would result in Nothing or Null itself.
$\therefore \phi \cap A = \phi$
$\therefore U' \cap A = \phi$

Note: When we are working with intersections and unions, we can use Venn diagrams and color them on paper or in mind and check for the area’s overlapping. Then we can easily find our result of any kind of intersection or union equations like these.