Question

The given equation is $x^2 + 4y^2 + 4y - 16 = 0$. Identify the conic section and provide its standard form.

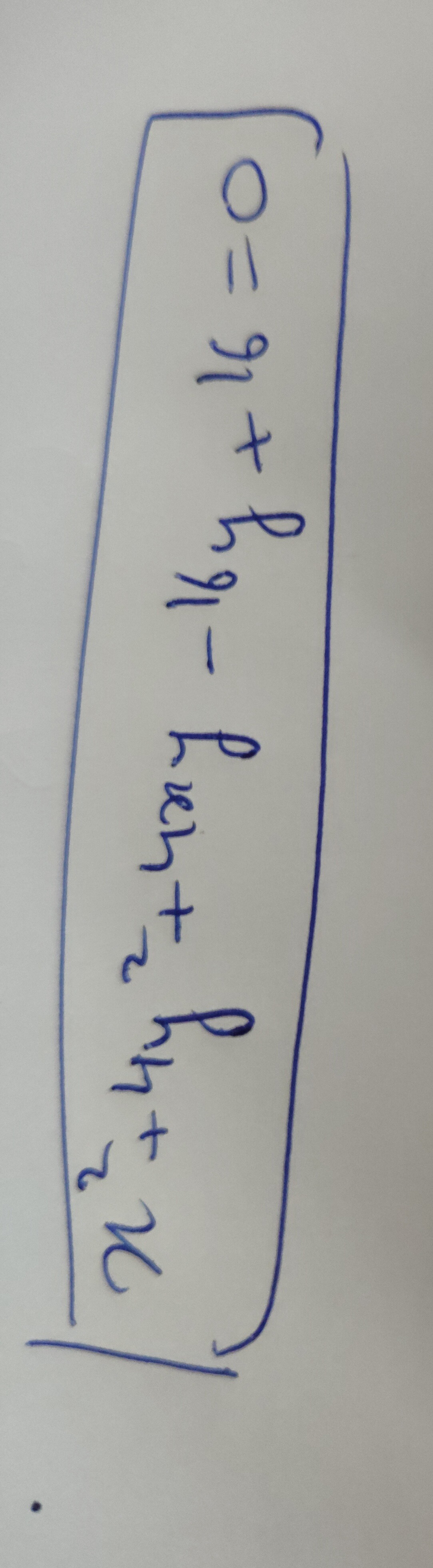
• A. The equation represents a parabola. The standard form is $x^2 = -4(y^2 + y - 4)$.
• B. The equation represents a hyperbola. The standard form is $\frac{x^2}{16} - \frac{4y^2}{16} = 1$.
• C. The equation represents an ellipse. The standard form is $\frac{x^2}{17} + \frac{\left(y + \frac{1}{2}\right)^2}{\frac{17}{4}} = 1$.
• D. The equation represents a circle. The standard form is $x^2 + y^2 = 16$.

Answer 1

Answer: (C)

The given equation $x^2 + 4y^2 + 4y - 16 = 0$ represents an ellipse. The standard form of the ellipse is: $\frac{x^2}{17} + \frac{\left(y + \frac{1}{2}\right)^2}{\frac{17}{4}} = 1$

Answer 2

To identify the conic section, we complete the square for the terms involving $y$: $4y^2 + 4y = 4\left(y^2 + y\right)$ $4\left(y^2 + y + \left(\frac{1}{2}\right)^2 - \left(\frac{1}{2}\right)^2\right) = 4\left(\left(y + \frac{1}{2}\right)^2 - \frac{1}{4}\right) = 4\left(y + \frac{1}{2}\right)^2 - 1$ Substitute this back into the original equation: $x^2 + \left(4\left(y + \frac{1}{2}\right)^2 - 1\right) - 16 = 0$ $x^2 + 4\left(y + \frac{1}{2}\right)^2 - 17 = 0$ Rearrange the terms to isolate the variables: $x^2 + 4\left(y + \frac{1}{2}\right)^2 = 17$ To obtain the standard form of a conic section, divide the entire equation by 17: $\frac{x^2}{17} + \frac{4\left(y + \frac{1}{2}\right)^2}{17} = 1$ $\frac{x^2}{17} + \frac{\left(y + \frac{1}{2}\right)^2}{\frac{17}{4}} = 1$ This equation is in the standard form of an ellipse: $\frac{(x-h)^2}{a^2} + \frac{(y-k)^2}{b^2} = 1$. The equation describes an ellipse centered at $(0, -1/2)$ with its major axis lying along the line $y = -1/2$.