Question
Question: $V_B=?$ $20 m/s$...
VB=? 20m/s
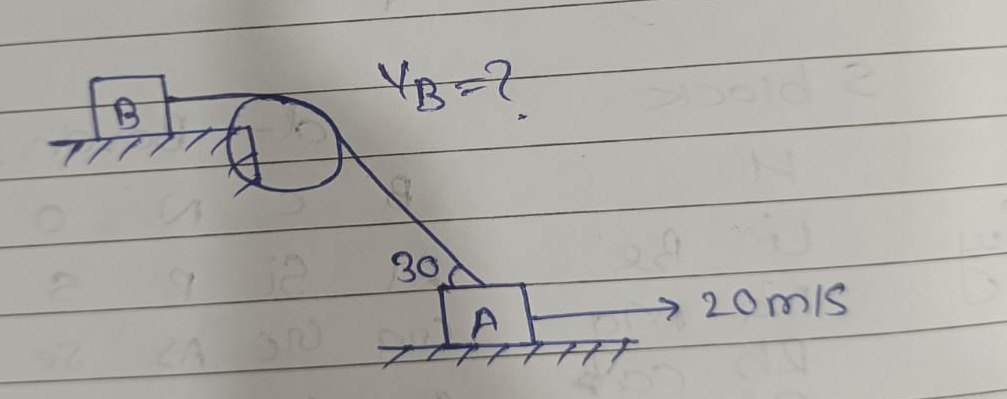
103m/s
Solution
This problem involves constrained motion, where the length of the string connecting the two blocks and the fixed pulley remains constant. We can solve this using the principle of velocity components along the string.
Let VA be the velocity of block A and VB be the velocity of block B. The string is inextensible, which means the component of velocity of any point on the string along the string must be the same.
-
Velocity component of block A along the string: Block A moves horizontally with velocity VA=20m/s. The string connected to block A makes an angle of 30∘ with the horizontal. Therefore, the component of VA along the string is VAcos(30∘). This component is directed away from the pulley.
-
Velocity component of block B along the string: Block B moves horizontally. The string connected to block B is also horizontal (assuming it's directly connected to the pulley horizontally). Therefore, the component of VB along the string is simply VB. This component is directed towards the pulley.
-
Equating the velocity components: For the string to remain taut and inextensible, the rate at which block A pulls the string away from the pulley must be equal to the rate at which block B pulls the string towards the pulley. Thus, we can equate the magnitudes of the velocity components along the string: VB=VAcos(30∘)
-
Substitute the given values: VA=20m/s cos(30∘)=23
VB=20×23 VB=103m/s
The velocity of block B is 103m/s. If block A moves to the right, block B will move to the left.
The problem is solved using the constraint that the length of the string is constant. The component of the velocity of block A along the string (VAcos30∘) must be equal to the velocity of block B along the string (VB), because the string is inextensible and passes over a fixed pulley. VB=VAcos30∘=20×23=103m/s.
