Question
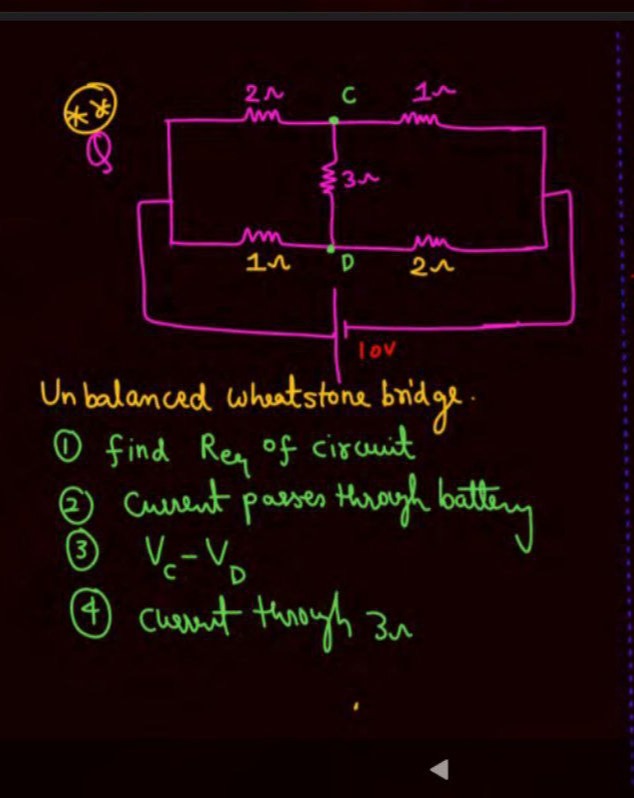
Question: Unbalanced wheatstone bridge. ① find $R_{eq}$ of circuit ② Current passes through battery ③ $V_c - ...
Unbalanced wheatstone bridge.
① find Req of circuit ② Current passes through battery ③ Vc−VD ④ current through 3Ω
- Req=913Ω
- Current passes through battery = 1390 A
- VC−VD=−1330 V
- Current through 3Ω = 1310 A (from D to C)
Solution
The circuit given is an unbalanced Wheatstone bridge. We will use Kirchhoff's laws to find the potentials at nodes C and D, and then calculate the required quantities.
Let the potential at the positive terminal of the battery be VP=10V and at the negative terminal be VQ=0V. The resistors are connected as follows:
- RPC=2Ω
- RCQ=1Ω
- RPD=1Ω
- RDQ=2Ω
- RCD=3Ω
Let VC and VD be the potentials at points C and D, respectively.
1. Apply Kirchhoff's Current Law (KCL) at nodes C and D:
-
At node C: Current entering C from P equals current leaving C towards D and Q. RPCVP−VC=RCDVC−VD+RCQVC−VQ 210−VC=3VC−VD+1VC−0 Multiply by 6 to clear denominators: 3(10−VC)=2(VC−VD)+6VC 30−3VC=2VC−2VD+6VC 30=11VC−2VD (Equation 1)
-
At node D: Current entering D from P and C equals current leaving D towards Q. RPDVP−VD+RCDVC−VD=RDQVD−VQ 110−VD+3VC−VD=2VD−0 Multiply by 6 to clear denominators: 6(10−VD)+2(VC−VD)=3VD 60−6VD+2VC−2VD=3VD 60+2VC−8VD=3VD 2VC−11VD=−60 (Equation 2)
2. Solve the system of linear equations for VC and VD: Equation 1: 11VC−2VD=30 Equation 2: 2VC−11VD=−60
Multiply Equation 1 by 11 and Equation 2 by 2: 121VC−22VD=330 4VC−22VD=−120
Subtract the second modified equation from the first: (121VC−4VC)−(22VD−22VD)=330−(−120) 117VC=450 VC=117450=39150=1350 V
Substitute VC back into Equation 1: 11(1350)−2VD=30 13550−2VD=30 2VD=13550−30=13550−390=13160 VD=1380 V
Now, let's answer the specific questions:
③ Find VC−VD VC−VD=1350−1380=−1330 V
④ Current through 3Ω resistor Current ICD=RCDVC−VD=3−30/13=−1310 A The negative sign indicates that the current flows from D to C. The magnitude of the current through the 3Ω resistor is 1310 A.
② Current passes through battery The total current from the battery is the sum of currents entering nodes C and D from P. Current IPC=RPCVP−VC=210−50/13=2(130−50)/13=280/13=1340 A Current IPD=RPDVP−VD=110−80/13=1(130−80)/13=1350 A Total current from battery Ibattery=IPC+IPD=1340+1350=1390 A
① Find Req of circuit The equivalent resistance is the total voltage divided by the total current. Req=IbatteryVbattery=90/1310=10×9013=90130=913Ω
