Question
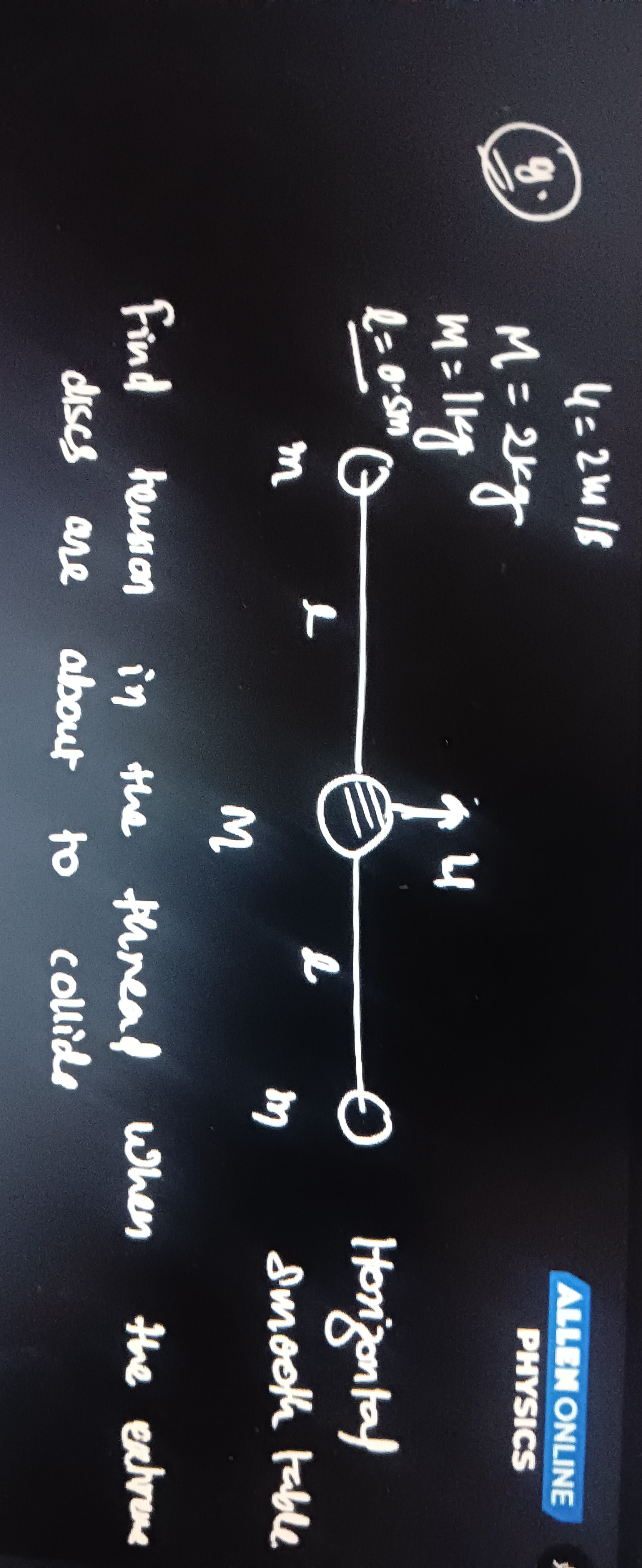
Question: Find tension in the thread when the extreme discs are about to collide....
Find tension in the thread when the extreme discs are about to collide.
4 N
Solution
1. System Description: The system consists of a central mass M and two identical outer masses m, connected by threads of length l. The central mass M is given an initial velocity u perpendicular to the threads on a smooth horizontal table. We need to find the tension in the threads when the outer masses are about to collide.
2. Coordinate System and Constraints: Let the initial position of the central mass M be at the origin (0,0). The initial positions of the outer masses are (−l,0) and (l,0). Let the positions at time t be M(0,yM), m1(−x,y), and m2(x,y). The constraint of constant thread length gives: x2+(yM−y)2=l2. The outer masses collide when x=0.
3. Conservation of Momentum: In the y-direction, the initial momentum is Mu. At any time t, the y-momentum is MvMy+mvm1y+mvm2y. Since vm1y=vm2y=y˙ and vMy=y˙M, we have: Mu=My˙M+2my˙.
4. Conservation of Energy: The initial kinetic energy is 21Mu2. At time t, the kinetic energy is 21MvM2+21mvm12+21mvm22. Since the motion is along the y-axis at the initial moment and later, vM2=y˙M2. The velocities of the outer masses are vm12=(−x˙)2+y˙2=x˙2+y˙2 and vm22=x˙2+y˙2. So, 21Mu2=21My˙M2+2×21m(x˙2+y˙2), which simplifies to Mu2=My˙M2+2m(x˙2+y˙2).
5. Constraint Differentiation: Differentiating x2+(yM−y)2=l2 with respect to time: 2xx˙+2(yM−y)(y˙M−y˙)=0⟹xx˙+(yM−y)(y˙M−y˙)=0.
6. Condition at Collision: Just before collision, x=0. From the constraint equation, (yM−y)2=l2, so ∣yM−y∣=l. Since the initial velocity is in the positive y-direction, yM>y, thus yM−y=l=0. The differentiated constraint equation at x=0 becomes (yM−y)(y˙M−y˙)=0, which implies y˙M−y˙=0, so y˙M=y˙.
7. Velocities at Collision: Substitute y˙M=y˙ into the momentum equation: Mu=My˙+2my˙=(M+2m)y˙⟹y˙=y˙M=M+2mMu. Substitute y˙M=y˙ into the energy equation: Mu2=My˙2+2m(x˙2+y˙2)=(M+2m)y˙2+2mx˙2. Mu2=(M+2m)(M+2mMu)2+2mx˙2. Mu2=M+2mM2u2+2mx˙2. 2mx˙2=Mu2−M+2mM2u2=Mu2(M+2mM+2m−M)=M+2m2mMu2. x˙2=M+2mMu2.
8. Tension Calculation: Consider the motion of an outer mass m relative to the central mass M. Just before collision, x=0, so the thread is along the y-axis. The relative velocity of m with respect to M is vm/M=vm−vM=(−x˙,y˙)−(0,y˙M)=(−x˙,0) since y˙=y˙M. The tangential velocity magnitude is vtan=∣x˙∣=M+2mMu2. The tension T provides the centripetal force for this relative motion: T=mlvtan2=mlx˙2=ml1(M+2mMu2).
9. Substituting Given Values: u=2 m/s, M=2 kg, m=1 kg, l=0.5 m. T=(1 kg)×0.5 m1×2 kg+2×(1 kg)(2 kg)×(2 m/s)2. T=2×2+22×4=2×48=2×2=4 N.
