Question

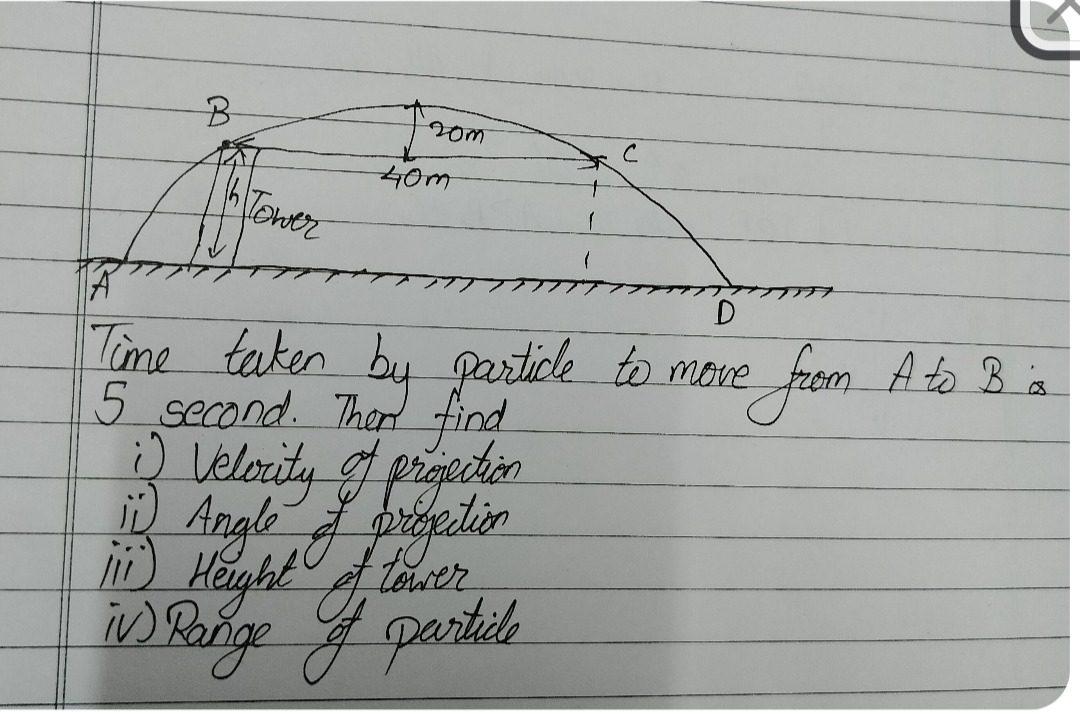
Time taken by particle to move from A to B is 5 second. Then find

ⅰ) Velocity of projection iⅱ) Angle of projection iii) Height of tower iv) Range of particle

Answer 1

Velocity of projection = 10\sqrt{29} m/s, Angle of projection = \arctan(\frac{5}{2}), Height of tower = 125 m, Range of particle = 200 m

Answer 2

The problem describes a projectile motion from point A on the ground. Point B is the highest point of the trajectory, and the time taken to reach B from A is 5 seconds. The height of the highest point B above the ground is denoted as $h_{Tower}$. Point C is on the trajectory such that the horizontal distance from B to C is 40m, and the vertical distance from B to C is 20m downwards. Point D is where the projectile lands on the ground.

Let the velocity of projection at A be $u$ at an angle $\theta$ with the horizontal. The time taken to reach the highest point B from A is given by $t_{AB} = \frac{u \sin \theta}{g}$. Given $t_{AB} = 5$ seconds. Assuming $g = 10 \, m/s^2$, we have $5 = \frac{u \sin \theta}{10}$, which gives $u \sin \theta = 50 \, m/s$.

The height of the highest point B above the ground is $h_{Tower}$. This is the maximum height of the projectile, $H_{max} = \frac{(u \sin \theta)^2}{2g}$. $h_{Tower} = \frac{(50)^2}{2 \times 10} = \frac{2500}{20} = 125 \, m$. So, the height of the tower is 125 m.

Point C is on the trajectory. The height of C above the ground is $y_C = h_{Tower} - 20 = 125 - 20 = 105 \, m$. Let $t_C$ be the time taken to reach point C from A. The vertical position of C is given by $y_C = (u \sin \theta) t_C - \frac{1}{2} g t_C^2$. $105 = 50 t_C - \frac{1}{2} \times 10 \times t_C^2$. $105 = 50 t_C - 5 t_C^2$. $5 t_C^2 - 50 t_C + 105 = 0$. $t_C^2 - 10 t_C + 21 = 0$. Factoring the quadratic equation, we get $(t_C - 3)(t_C - 7) = 0$. So, $t_C = 3$ seconds or $t_C = 7$ seconds. Since point C is after the highest point B (reached at $t=5$ seconds), the time taken to reach C must be greater than 5 seconds. Thus, $t_C = 7$ seconds.

Let $x_B$ be the horizontal distance of B from A, and $x_C$ be the horizontal distance of C from A. The horizontal velocity is constant, $u_x = u \cos \theta$. $x_B = (u \cos \theta) t_{AB} = (u \cos \theta) \times 5$. $x_C = (u \cos \theta) t_C = (u \cos \theta) \times 7$. The horizontal distance from B to C is given as 40m. Since C is to the right of B, $x_C - x_B = 40$. $7 (u \cos \theta) - 5 (u \cos \theta) = 40$. $2 (u \cos \theta) = 40$. $u \cos \theta = 20 \, m/s$.

Now we have $u \sin \theta = 50 \, m/s$ and $u \cos \theta = 20 \, m/s$. ⅰ) Velocity of projection $u = \sqrt{(u \sin \theta)^2 + (u \cos \theta)^2} = \sqrt{50^2 + 20^2} = \sqrt{2500 + 400} = \sqrt{2900} = 10 \sqrt{29} \, m/s$. iⅱ) Angle of projection $\theta = \arctan\left(\frac{u \sin \theta}{u \cos \theta}\right) = \arctan\left(\frac{50}{20}\right) = \arctan\left(\frac{5}{2}\right)$. iii) Height of tower $h_{Tower} = 125 \, m$. iv) Range of particle. The range is the horizontal distance from A to D, where D is the point where the projectile lands on the ground. The time of flight from A to D is the time when the vertical position is 0. $y(t) = (u \sin \theta) t - \frac{1}{2} g t^2 = 0$. $t((u \sin \theta) - \frac{1}{2} g t) = 0$. The solutions are $t=0$ (at A) and $t = \frac{2 u \sin \theta}{g}$. Time of flight $T = \frac{2 \times 50}{10} = 10$ seconds. The range is $R = (u \cos \theta) T = 20 \times 10 = 200 \, m$.

Explanation of the solution:

1. Time to reach the highest point gives the vertical component of initial velocity.
2. Maximum height is calculated from the vertical component of initial velocity. This is the height of the tower.
3. Using the coordinates of point C and the equation of trajectory, find the time to reach C.
4. Using the horizontal distance between B and C and the time difference between reaching B and C, find the horizontal component of initial velocity.
5. Calculate the magnitude and angle of initial velocity from its components.
6. Calculate the time of flight and range using the initial velocity components.