Question

T₁

2Kg

T₂

3Kg

T₃

5Kg

2m/s²

Answer 1

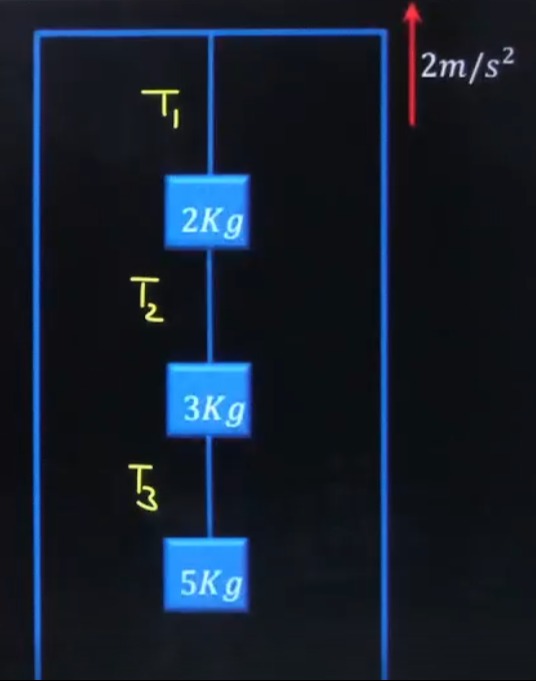
T₁ = 120 N, T₂ = 96 N, T₃ = 60 N

Answer 2

The problem involves three masses suspended by strings, accelerating upwards. We need to find the tension in each string (T₁, T₂, T₃).

Given:

• Masses: $m_1 = 2 \text{ Kg}$, $m_2 = 3 \text{ Kg}$, $m_3 = 5 \text{ Kg}$
• Acceleration of the system: $a = 2 \text{ m/s}^2$ (upwards)
• Assume acceleration due to gravity: $g = 10 \text{ m/s}^2$

We will apply Newton's second law ($F_{net} = ma$) to different sections of the system.

1. Calculate T₃ (Tension between 3 Kg and 5 Kg masses): Consider the lowest mass, $m_3 = 5 \text{ Kg}$. Forces acting on $m_3$:

• Tension $T_3$ acting upwards.
• Weight $m_3g$ acting downwards. Since the mass is accelerating upwards, the net force is upwards.

$T_3 - m_3g = m_3a$ $T_3 = m_3(g + a)$ Substitute the values: $T_3 = 5 \text{ Kg} \times (10 \text{ m/s}^2 + 2 \text{ m/s}^2)$ $T_3 = 5 \text{ Kg} \times 12 \text{ m/s}^2$ $T_3 = 60 \text{ N}$

2. Calculate T₂ (Tension between 2 Kg and 3 Kg masses): Consider the combined system of masses ($m_2 + m_3$). Total mass = $m_2 + m_3 = 3 \text{ Kg} + 5 \text{ Kg} = 8 \text{ Kg}$. Forces acting on this combined system:

• Tension $T_2$ acting upwards.
• Total weight $(m_2 + m_3)g$ acting downwards. Since the system is accelerating upwards:

$T_2 - (m_2 + m_3)g = (m_2 + m_3)a$ $T_2 = (m_2 + m_3)(g + a)$ Substitute the values: $T_2 = (3 \text{ Kg} + 5 \text{ Kg}) \times (10 \text{ m/s}^2 + 2 \text{ m/s}^2)$ $T_2 = 8 \text{ Kg} \times 12 \text{ m/s}^2$ $T_2 = 96 \text{ N}$

3. Calculate T₁ (Tension at the top string): Consider the entire system of masses ($m_1 + m_2 + m_3$). Total mass = $m_1 + m_2 + m_3 = 2 \text{ Kg} + 3 \text{ Kg} + 5 \text{ Kg} = 10 \text{ Kg}$. Forces acting on the entire system:

• Tension $T_1$ acting upwards.
• Total weight $(m_1 + m_2 + m_3)g$ acting downwards. Since the entire system is accelerating upwards:

$T_1 - (m_1 + m_2 + m_3)g = (m_1 + m_2 + m_3)a$ $T_1 = (m_1 + m_2 + m_3)(g + a)$ Substitute the values: $T_1 = (2 \text{ Kg} + 3 \text{ Kg} + 5 \text{ Kg}) \times (10 \text{ m/s}^2 + 2 \text{ m/s}^2)$ $T_1 = 10 \text{ Kg} \times 12 \text{ m/s}^2$ $T_1 = 120 \text{ N}$

Summary of Tensions:

• $T_1 = 120 \text{ N}$
• $T_2 = 96 \text{ N}$
• $T_3 = 60 \text{ N}$

---

Solution:

1. Tension T₃: Consider the 5 Kg mass. $T_3 - m_3g = m_3a \implies T_3 = m_3(g+a) = 5(10+2) = 5 \times 12 = 60 \text{ N}$.
2. Tension T₂: Consider the (3 Kg + 5 Kg) system. $T_2 - (m_2+m_3)g = (m_2+m_3)a \implies T_2 = (m_2+m_3)(g+a) = (3+5)(10+2) = 8 \times 12 = 96 \text{ N}$.
3. Tension T₁: Consider the (2 Kg + 3 Kg + 5 Kg) system. $T_1 - (m_1+m_2+m_3)g = (m_1+m_2+m_3)a \implies T_1 = (m_1+m_2+m_3)(g+a) = (2+3+5)(10+2) = 10 \times 12 = 120 \text{ N}$.