Question

T=?

Answer 1

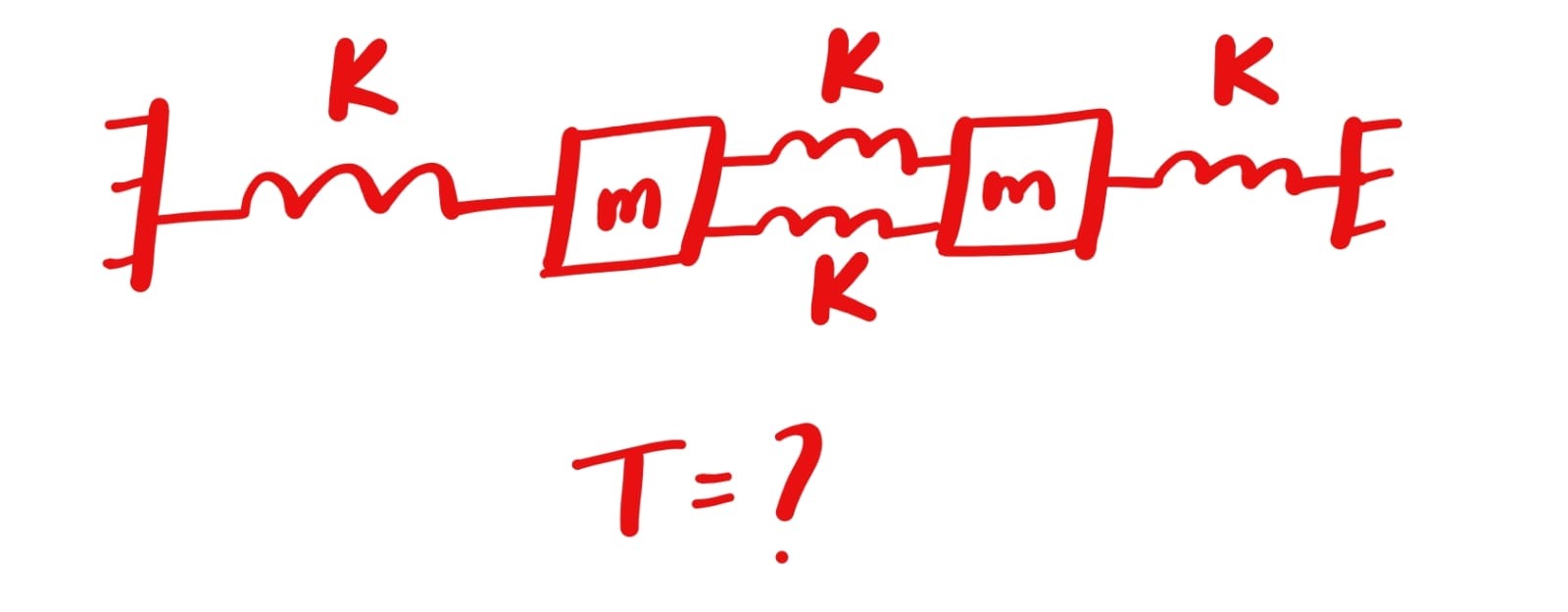
There are two normal modes:

• For masses oscillating in-phase: T = 2π√(m/k)
• For masses oscillating out-of-phase: T = 2π√(m/(5k))

Answer 2

We begin by writing the total potential energy for small displacements. Let x and y denote the displacements (from equilibrium) of the left and right masses, respectively. Then the potential energies are:

• Left wall spring: ½ k x²
• Right wall spring: ½ k y²
• Two identical springs connecting the masses, each stretched by (y – x): 2 × ½ k (y – x)² = k (y – x)²

Thus, the total potential energy is

  U = ½ k x² + ½ k y² + k (y – x)².

Expanding, we have

  U = ½ k x² + ½ k y² + k (x² – 2xy + y²)     = (3/2)k x² + (3/2)k y² – 2kxy.

The kinetic energy is

  T = ½ m (ẋ² + ẏ²).

Using Lagrange’s equations (or by writing the equations of motion), we obtain the coupled equations:

  m x¨ = – (3k x – 2k y)   m y¨ = – (3k y – 2k x).

Assuming solutions of the form x = A cos ωt, y = B cos ωt, we substitute to get

  (3k – mω²)A – 2k B = 0,   –2k A + (3k – mω²)B = 0.

Non‐trivial solutions require a zero determinant:

  (3k – mω²)² – (2k)² = 0 ⟹ 3k – mω² = ± 2k.

Thus, we have two cases:

1. For 3k – mω² = 2k ⟹ mω² = k ⟹ ω₁ = √(k/m).
     This is the in‐phase (symmetric) mode (since then A = B).

2. For 3k – mω² = –2k ⟹ mω² = 5k ⟹ ω₂ = √(5k/m).
     This is the out‐of‐phase (antisymmetric) mode (since A = –B).

Since the period T is related to ω by T = 2π/ω, the two modes have periods:

  • Symmetric mode: T₁ = 2π√(m/k)
  • Antisymmetric mode: T₂ = 2π√(m/(5k))