Question

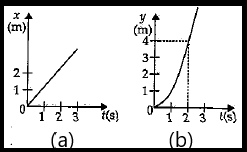
Figure shows (x, t), (y, t) diagram of a particle moving in 2- dimensions. If the particle has a mass of 500 g, the force acting on the particle is

A.) 1 N along y- axis
B.) 1 N along x- axis
C.) 0.5 N along x- axis
D.) 0.5 N along y- axis

Answer 1

Hint: The graph between x and t is a straight line which is passing through origin, so we can write $x = t$. Also, the other graph between y and t is a parabola, so we can write $y = {t^2}$ , then differentiate the given equations to find the acceleration and then force.

Complete step-by-step answer:

Formula used - ${v_x} = \dfrac{{dx}}{{dt}}$ , ${a_x} = \dfrac{{d{v_x}}}{{dt}}$ , ${v_y} = \dfrac{{dy}}{{dt}}$ , ${a_y} = \dfrac{{d{v_y}}}{{dt}}$ , $F = m{a_y}$

We have been shown in the figures above, a particle moving in 2-D.

The mass of the particle is given to be 500 g.

So, to find the force acting on the particle, we will be using the formula, F = ma, where m is the mass of the particle and a is acceleration of the particle.

So, to find the force acting on the particle, we will first find the acceleration.
Now refer to the figure given in question shown below-

Now in the figure (a), the graph is between x and t, as we can see the graph is a straight line passing through the origin, so the equation will be $x = t$ .
Now, in figure (b), the graph is between y and t, as we can see the graph is a curve passing through origin, so the equation will be $y = {t^2}$ .

now, using $x = t$ ,we can find the velocity by differentiating the equation-

So, we get- ${v_x} = \dfrac{{dx}}{{dt}} = 1$

Differentiating again we will get the acceleration along x- axis-

${a_x} = \dfrac{{d{v_x}}}{{dt}} = 0$

now, using the equation $y = {t^2}$ , and then differentiating wrt to t, we get the velocity along y- axis-

${v_y} = \dfrac{{dy}}{{dt}} = 2t$

Now again differentiating wrt to t we will get the acceleration along y- axis-

${a_y} = \dfrac{{d{v_y}}}{{dt}} = 2 \\\ \Rightarrow {a_y} = 2m/{s^2} \\\$

now, as we can see the acceleration along the x- axis is zero, since, ${a_x} = \dfrac{{d{v_x}}}{{dt}} = 0$ , so no force along x- axis.

But the acceleration along y- axis is 2 m/s2.

So, the force acting on the particle is-

$F = m{a_y}$

Putting m = 500 g = 0.5 Kg {since 1 kg = 1000g} and ${a_y} = 2m/{s^2}$ .
We get-

$F = 0.5 \times 2 = 1N$ along y- axis.

Hence, the correct option is A.

Note – Whenever such types of questions appear, first write down the things given in the question and then use the graphs from equations of the graph in figure (a) and (b). Then, find the acceleration of the particle along the x- axis and y- axis by differentiating the velocity found, as mentioned in the solution. Then, find the force acting on the particle.