Question

Figure shows variation of $R$, ${{X}_{L}}$ and ${{X}_{C}}$ with frequency $f$ in a series LCR circuit. Then for what frequency point the circuit is inductive?

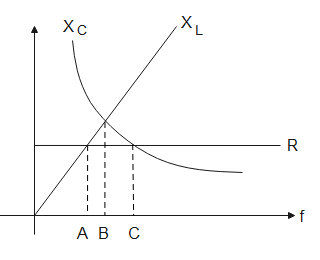
(1). A
(2). B
(3). C
(4). all points

Answer 1

An AC circuit consisting of a capacitor, inductor and resistor connected together is known as LCR circuit. Ohm’s law can be applied to this circuit. The reactance in the circuit depends on the inductive reactance, capacitive reactance and resistance. In an inductive circuit, the inductance reactance is more than the capacitive reactance.

Complete answer:
An L, C, R circuit is a circuit which contains a capacitor, an inductor and a resistance connected together. The total reactance in the circuit is given by-
$Z=\sqrt{{{R}^{2}}+{{({{X}_{L}}-{{X}_{C}})}^{2}}}$
Here, $Z$ is the total reactance in the circuit
$R$ is the resistance
${{X}_{L}}$ is the inductive reactance
${{X}_{C}}$ is the capacitive reactance
A circuit is known as an inductive circuit when the value of inductance in the circuit is more than the value of capacitance. The value of inductance increases after resonance frequency is attained.
The resonance in a circuit is achieved when the inductive reactance and the capacitive reactance are equal to each other. Therefore,
${{X}_{L}}={{X}_{C}}$

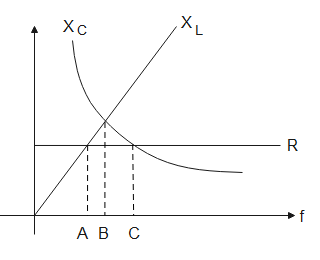
In the graph, at the point C, ${{X}_{L}}$ is greater than ${{X}_{C}}$ because this is the point after the resonance condition is attained.
Therefore, the circuit is inductive at point C in the graph.

Hence, the correct option is (3).

Note:
AC current flows in a LCR circuit. During resonance, the current is the circuit suddenly increases to its highest value as the reactance in the circuit is minimum. A capacitor stores charge on it while an inductor opposes the change in the magnitude or direction of current in the circuit. The resonant frequency of a circuit depends on the value of inductance and capacitance in the circuit.