Question

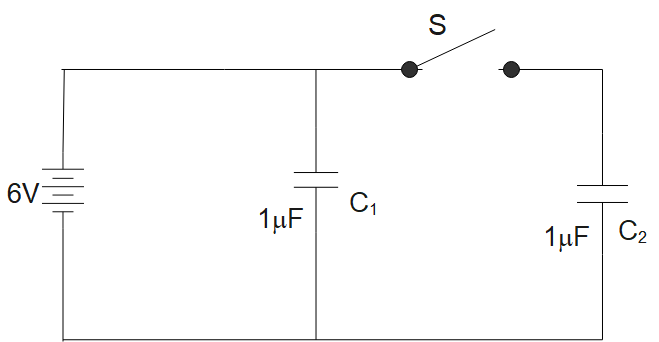
Figure shows two identical capacitors, ${{C}_{1}}$ and ${{C}_{2}}$ each of $1\mu F$ capacitance connected to a battery of 6V. Initially switch “S” is closed. After sometime switch “S” is left open and dielectric slabs of dielectric constant K=3 is inserted to fill completely the space between the plates of the two capacitors how will the (i) Charge and (ii) the potential difference between the plates of the capacitors affected after the slabs are inserted.

Answer 1

As we can see in the figure, the switch “S” only affects the capacitor ${{C}_{2}}$, and the capacitor ${{C}_{1}}$ remains unaffected from it because the switch only breaks the connection in between the battery and the capacitor ${{C}_{2}}$ keeping the capacitor ${{C}_{1}}$ to its original state, But adding dielectric affects both the capacitors in the same way.

Complete step-by-step solution:
We know that the potential difference between the capacitor is 6V when the switch is kept closed. It is given in the question that we have a 6V battery connected to the network.
${{V}_{1}}={{V}_{2}}=6V$
We have also been given that both the capacitors are of same capacitance. So,
${{C}_{1}}={{C}_{2}}=1\mu F$
Now, when the switch is closed, charge on each of the capacitors will be the same as they are connected to the same battery and have the same capacitance.
So, we can say that
${{Q}_{1}}={{Q}_{2}}=CV$
$CV=(1\mu F)\times (6V)$
$CV=6\mu C$
Or we can say that
${{Q}_{1}}={{Q}_{2}}=6\mu C$
Now, the question tells us that the switch is open now and as we can see in the figure that opening and closing only impact the capacitor ${{C}_{2}}$ and it does not have any effect on capacitor ${{C}_{1}}$. Therefore, the potential difference across the capacitor ${{C}_{1}}$ will be the same.
But the question also told us that a dielectric has been inserted in between the plates so now capacitance of both the capacitors will change
We have been given that the dielectric constant is K= 3
$C_{1}^{*}=C_{2}^{*}=3\times 1\mu F$
$C_{1}^{*}=C_{2}^{*}=3\mu F$
(i)
Now the charge on capacitor ${{C}_{1}}$ will be
${{Q}_{1}}=C_{1}^{*}{{V}_{1}}$
${{Q}_{1}}=3\times 6$
${{Q}_{1}}=18\mu F$
The charge on the capacitor ${{C}_{1}}$ will not be affected as, when the switch “S” is kept open the capacitor ${{C}_{2}}$ is not in the circuit.
(ii) Now potential difference across ${{C}_{1}}$ will remain same
Potential difference across ${{C}_{2}}$ will be
$V_{2}^{*}=\dfrac{{{Q}_{2}}}{C_{2}^{*}}$
$V_{2}^{*}=\dfrac{6}{3}$
$V_{2}^{*}=2V$

Note: In this question, the switch “S” is kept closed initially and when the switch is closed the capacitors charge themselves to their full capacity but when the switch is kept open then the 2nd capacitor or capacitor ${{C}_{2}}$ will be out of circuit. Also, it does not have any load resistance hence it cannot discharge itself.