Question

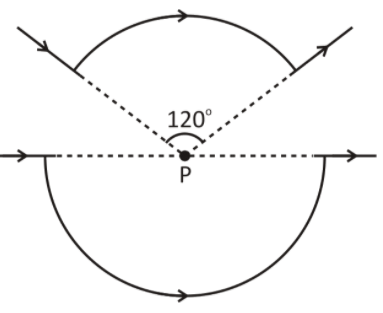
Figure shows two current segments. In the upper segment, an arc of radius 4 cm subtends an angle of 120° with centre P. The lower segment includes a large semicircle of radius 5 cm also with centre P. If I = 0.4 amp in both. If the net magnetic field at point P due to these current segments is $\dfrac{{\pi x}}{{30}}\mu T$ then find the value of x.

Answer 1

First find the magnetic field at P due to the upper segment. Then, find the magnetic field at P due to the lower segment. Subtract them to find the net magnetic field and compare the result with the given relation. Use the appropriate to find the magnetic field induction at P.

Complete step by step answer:
Magnetic field induction at P due to the upper segment
Here, the angle made by the current carrying arc at the centre $\theta = 120^\circ \Rightarrow \theta = \dfrac{{2\pi }}{3}$ radians.
Current flowing in the segment, I = 0.4 A
Radius, r = 5 cm = 0.05 m
Magnetic field induction at the point P is given by the relation$\overrightarrow B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{I}{r}\theta$
$\Rightarrow \overrightarrow {{B_1}} = {10^{ - 7}} \times \dfrac{{0.4}}{{0.05}} \times \dfrac{{2\pi }}{3}$
$\Rightarrow \overrightarrow {{B_1}} = \dfrac{{8\pi }}{{15}} \times {10^{ - 6}} = \dfrac{{8\pi }}{{15}}\,\mu T = \dfrac{{16\pi }}{{30}}\,\mu T$
Here, the direction of the magnetic field induction is outside the plane of paper.
Magnetic field induction at P due to the lower segment
Here, the angle made by the current carrying arc at the centre $\theta = 180^\circ \Rightarrow \theta = \pi$ radians.
Current flowing in the segment, I = 0.4 A
Radius, r = 5 cm = 0.05 m
Magnetic field induction at the point P is given by the relation$\overrightarrow B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{I}{r}\theta$
$\Rightarrow \overrightarrow {{B_2}} = {10^{ - 7}} \times \dfrac{{0.4}}{{0.05}} \times \pi$
$\Rightarrow \overrightarrow {{B_2}} = \dfrac{{4\pi }}{5} \times {10^{ - 6}} = \dfrac{{4\pi }}{5}\mu T = \dfrac{{24\pi }}{{30}}\mu T$
Here, the direction of the magnetic field is inside the plane of paper.
Net magnetic field at Point P is $\overrightarrow B = \overrightarrow {{B_2}} - \overrightarrow {{B_1}}$
$\Rightarrow \overrightarrow B = \dfrac{{24\pi }}{{30}}\mu T - \dfrac{{16\pi }}{{30}}\mu T = \dfrac{{8\pi }}{{30}}\mu T$
The direction of the magnetic field induction is inside the plane of paper.
Comparing it with the equation $\dfrac{{\pi x}}{{30}}\mu T$, we get x = 8.

Note:
The direction of the magnetic field due to a circular arc depends on the direction of the current flowing in the coil. The direction of the magnetic field is found by the Right hand thumb rule. If the direction of the current is in the clockwise direction, the magnetic field points into the plane of paper. If it is in the anticlockwise direction. The magnetic field will points towards the plane of paper.