Question

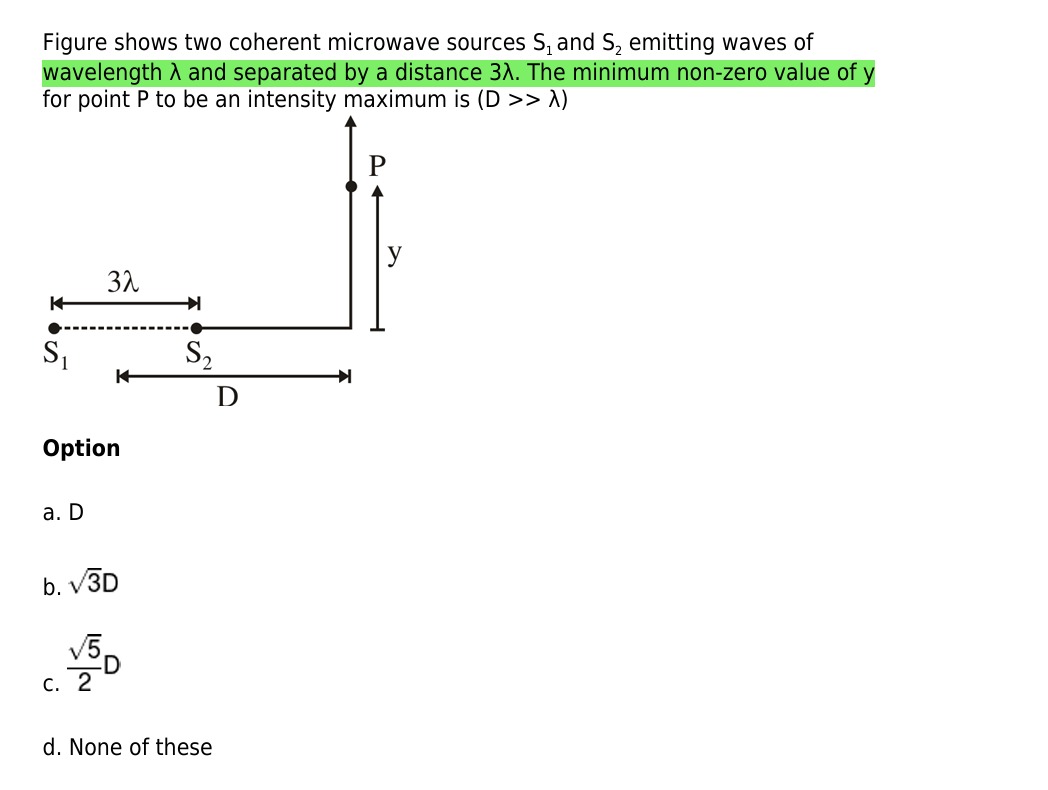
Figure shows two coherent microwave sources $S_1$ and $S_2$ emitting waves of wavelength $\lambda$ and separated by a distance $3\lambda$. The minimum non-zero value of y for point P to be an intensity maximum is (D >> $\lambda$)

• A. D
• B. $\sqrt{3}D$
• C. $\frac{\sqrt{5}}{2}D$
• D. None of these

Answer 1

Answer: (C)

$\frac{\sqrt{5}}{2}D$

Answer 2

The path difference between the waves from $S_1$ and $S_2$ to point P is given by $\Delta r = r_1 - r_2$, where $r_1$ is the distance from $S_1$ to P and $r_2$ is the distance from $S_2$ to P.

Let $S_2$ be at the origin (0, 0). Then $S_1$ is at $(-3\lambda, 0)$ and P is at $(D, y)$. $r_1 = \sqrt{(D - (-3\lambda))^2 + (y - 0)^2} = \sqrt{(D + 3\lambda)^2 + y^2}$ $r_2 = \sqrt{(D - 0)^2 + (y - 0)^2} = \sqrt{D^2 + y^2}$

For constructive interference (intensity maximum), the path difference must be an integer multiple of the wavelength: $r_1 - r_2 = n\lambda$, where $n = 0, 1, 2, ...$. $\sqrt{(D + 3\lambda)^2 + y^2} - \sqrt{D^2 + y^2} = n\lambda$ $\sqrt{(D + 3\lambda)^2 + y^2} = \sqrt{D^2 + y^2} + n\lambda$

Square both sides: $(D + 3\lambda)^2 + y^2 = (\sqrt{D^2 + y^2} + n\lambda)^2$ $D^2 + 6D\lambda + 9\lambda^2 + y^2 = (D^2 + y^2) + (n\lambda)^2 + 2n\lambda \sqrt{D^2 + y^2}$ $D^2 + 6D\lambda + 9\lambda^2 + y^2 = D^2 + y^2 + n^2\lambda^2 + 2n\lambda \sqrt{D^2 + y^2}$ $6D\lambda + 9\lambda^2 - n^2\lambda^2 = 2n\lambda \sqrt{D^2 + y^2}$

Divide by $\lambda$ (assuming $\lambda \ne 0$): $6D + 9\lambda - n^2\lambda = 2n \sqrt{D^2 + y^2}$ $6D + (9 - n^2)\lambda = 2n \sqrt{D^2 + y^2}$

Square both sides: $(6D + (9 - n^2)\lambda)^2 = (2n \sqrt{D^2 + y^2})^2$ $36D^2 + 12D(9 - n^2)\lambda + (9 - n^2)^2\lambda^2 = 4n^2 (D^2 + y^2)$ $36D^2 + 12D(9 - n^2)\lambda + (9 - n^2)^2\lambda^2 = 4n^2D^2 + 4n^2y^2$ $4n^2y^2 = 36D^2 - 4n^2D^2 + 12D(9 - n^2)\lambda + (9 - n^2)^2\lambda^2$ $4n^2y^2 = (36 - 4n^2)D^2 + 12D(9 - n^2)\lambda + (9 - n^2)^2\lambda^2$

We are given $D >> \lambda$. We are looking for the minimum non-zero value of y. Let's analyze the equation for different values of n. For n=0, $0 = 36D^2 + 108D\lambda + 81\lambda^2 = (6D + 9\lambda)^2$. This implies $6D + 9\lambda = 0$, which is not possible for positive D and $\lambda$. So n=0 does not give a solution for y.

For n=1: $4(1)^2y^2 = (36 - 4(1)^2)D^2 + 12D(9 - 1^2)\lambda + (9 - 1^2)^2\lambda^2$ $4y^2 = (36 - 4)D^2 + 12D(8)\lambda + (8)^2\lambda^2$ $4y^2 = 32D^2 + 96D\lambda + 64\lambda^2$ $y^2 = 8D^2 + 24D\lambda + 16\lambda^2$ $y = \sqrt{8D^2 + 24D\lambda + 16\lambda^2}$. Since $D >> \lambda$, $y \approx \sqrt{8D^2} = \sqrt{8}D = 2\sqrt{2}D$.

For n=2: $4(2)^2y^2 = (36 - 4(2)^2)D^2 + 12D(9 - 2^2)\lambda + (9 - 2^2)^2\lambda^2$ $16y^2 = (36 - 16)D^2 + 12D(5)\lambda + (5)^2\lambda^2$ $16y^2 = 20D^2 + 60D\lambda + 25\lambda^2$ $y^2 = \frac{20}{16}D^2 + \frac{60}{16}D\lambda + \frac{25}{16}\lambda^2$ $y^2 = \frac{5}{4}D^2 + \frac{15}{4}D\lambda + \frac{25}{16}\lambda^2$ $y = \sqrt{\frac{5}{4}D^2 + \frac{15}{4}D\lambda + \frac{25}{16}\lambda^2}$. Since $D >> \lambda$, $y \approx \sqrt{\frac{5}{4}D^2} = \sqrt{\frac{5}{4}}D = \frac{\sqrt{5}}{2}D$.

For n=3: $4(3)^2y^2 = (36 - 4(3)^2)D^2 + 12D(9 - 3^2)\lambda + (9 - 3^2)^2\lambda^2$ $36y^2 = (36 - 36)D^2 + 12D(0)\lambda + (0)^2\lambda^2$ $36y^2 = 0$ $y = 0$. This is a possible solution for n=3, but we are looking for a non-zero value of y.

For n=4: $4(4)^2y^2 = (36 - 4(4)^2)D^2 + 12D(9 - 4^2)\lambda + (9 - 4^2)^2\lambda^2$ $64y^2 = (36 - 64)D^2 + 12D(9 - 16)\lambda + (9 - 16)^2\lambda^2$ $64y^2 = -28D^2 - 84D\lambda + 49\lambda^2$ Since $D >> \lambda$, the term $-28D^2$ dominates the right side, which is negative. Thus, $y^2 < 0$, which means there is no real solution for y when $n=4$. In general, for $n \ge 3$, $36 - 4n^2 \le 0$. If $36 - 4n^2 < 0$, then the term $(36 - 4n^2)D^2$ is negative and proportional to $D^2$. The other terms are proportional to $D\lambda$ or $\lambda^2$. Since $D >> \lambda$, the term proportional to $D^2$ will dominate. For $y^2$ to be non-negative, we need $(36 - 4n^2)D^2 + 12D(9 - n^2)\lambda + (9 - n^2)^2\lambda^2 \ge 0$. If $36 - 4n^2 < 0$, i.e., $n^2 > 9$, then for large D, the term $(36 - 4n^2)D^2$ is a large negative number, while the other terms are of lower order in D. So for $n \ge 4$, $y^2$ will be negative. Thus, the possible positive integer values of n are 1 and 2.

For n=1, $y \approx 2\sqrt{2}D \approx 2.828D$. For n=2, $y \approx \frac{\sqrt{5}}{2}D \approx 1.118D$. The minimum non-zero value of y occurs for n=2, and is approximately $\frac{\sqrt{5}}{2}D$.

Let's check the exact values. For n=1, $y = \sqrt{8D^2 + 24D\lambda + 16\lambda^2}$. For n=2, $y = \sqrt{\frac{5}{4}D^2 + \frac{15}{4}D\lambda + \frac{25}{16}\lambda^2}$. Since $D >> \lambda$, the terms with $\lambda$ are small compared to the term with $D^2$. So the minimum value of y is indeed approximately $\frac{\sqrt{5}}{2}D$. Comparing the options, option (c) is $\frac{\sqrt{5}}{2}D$.