Question

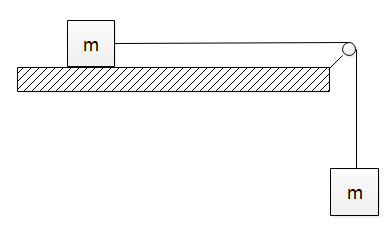
Figure shows two blocks each of masses $m$ connected by a string passing over a pulley. The horizontal table is smooth. The pulley has a radius $r$ and moment of inertia $I$ Find the acceleration of the hanging mass

A) $a = \dfrac{{mg}}{{2m + \dfrac{1}{{{r^2}}}}}$
B) $a = \dfrac{{mg}}{{m + \dfrac{1}{{{r^2}}}}}$
C) $a = \dfrac{{2mg}}{{2m + \dfrac{1}{{{r^2}}}}}$
D) $a = \dfrac{{mg}}{{m + \dfrac{1}{{{r^2}}}}}$

Answer 1

In this solution, we will first calculate the tension in the string on the left side and below the pulley. Then we will use the relation of torque and angular acceleration to determine the acceleration of the hanging mass.

Formula used: In this solution, we will use the following formula:
Torque of the pulley: $\tau = F.r = I.\alpha$ where $F$ is the force on the pulley, $r$ is the radius of the pulley, $I$ is the moment of inertia of the rod, and $\alpha$ is the angular acceleration of the pulley.

Complete step by step answer
In the diagram given to us, the block on the flat surface will move to the right since there is no friction and the string will rotate over the pulley.
Let the tension in the string on the left of the pulley will be ${T_1}$ and the tension in the string below the pulley be ${T_2}$ and the acceleration of both the masses be $a$ . The equation of motion of the top mass will be
${T_1} = ma$
And for the lower mass which is falling down will be
$Mg - {T_2} = Ma$
Hence the force acting on the pulley will be
$F = {T_2} - {T_1}$
The torque acting on the pulley will be determined from $\tau = F.r = I.\alpha$ as
$({T_2} - {T_1})r = I\alpha$
Now, as $\alpha = a/r$ , we have
$({T_2} - {T_1})r = \dfrac{{Ia}}{r}$
Substituting the values of ${T_1}$ and ${T_2}$ , we get
$mg - 2ma = \dfrac{{Ia}}{{{r^2}}}$
Solving for $a$ , we get
$a = \dfrac{{mg}}{{2m + \dfrac{I}{{{r^2}}}}}$ which corresponds to option (A).

Note
Here we must realize that the acceleration of the two blocks will be the same since they are connected by a string. Also, the tension on two sides of the pulley will be unequal since the string will be rotating on the pulley without slipping.