Question

Figure shows two adiabatic vessels, each containing a mass m of water at different temperatures. The ends of a metal rod of length L, area of cross section A and thermal conductivity K, are inserted in the water as shown in the figure. Find the time taken for the difference between the temperatures in the vessels to become half of the original value. The specific heat capacity of water is s. Neglect the heat capacity of the rod and the container and any loss of heat to the atmosphere.

Answer 1

Here we have given a system containing two vessels which are connected with rod and we have to find the time taken by the system to reduce the temperature difference between the vessels by half of its original value. As the vessels are attached to each other by rod there would be heat transfer from the rod. By measuring the heat transfer through the rod and heat loss by water in one vessel and heat gained by water in another vessel we can get our solution.

Formula used:

& \dfrac{dQ}{dt}=\dfrac{KA({{T}_{1}}-{{T}_{2}})}{l} \\\ & \text{Heat loss, }dQ=ms({{T}_{i}}-{{T}_{f}}) \\\ & \text{Heat gain, }dQ=ms({{T}_{f}}-{{T}_{i}}) \\\ \end{aligned}$$ **Complete answer:** According to the question, two vessels say 1 and 2 having water of mass m in each at different temperature, say $${{T}_{1}}\text{ and }{{T}_{2}}$$respectively are connected by a rod. Because the water in the vessel is at a different temperature there will be heat transfer across it. Let us redraw above diagram and label it. 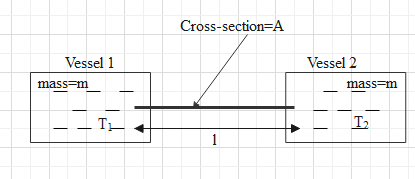 Let us assume that heat transfers from vessel 1 to vessel 2, then the rate at which the heat will transfer across the rod can be given as $$\dfrac{dQ}{dt}=\dfrac{KA({{T}_{1}}-{{T}_{2}})}{l}\text{ }.............\text{(i)}$$ Where K is thermal conductivity of rod, A is the cross sectional area of the rod and l is the length of the rod. As heat is flowing from vessel 1 to vessel 2, there will be heat loss by water and heat loss is given as $$dQ=ms({{T}_{i}}-{{T}_{f}})$$ Where m is mass of the substance, s is specific heat of substance, $${{T}_{i}}$$is the initial temperature of the substance and $${{T}_{f}}$$is the final temperature. Now heat loss by water in vessel 1, if $${{T}_{1}}$$ is initial temperature and $$T{{'}_{1}}$$is final temperature and it is given that mass of water is m and it specific heat is s, then $$dQ=ms({{T}_{1}}-T{{'}_{1}})$$ Now using equation (i) we can write the above equation as $$\begin{aligned} & ms({{T}_{1}}-T{{'}_{1}})=\dfrac{KA({{T}_{1}}-{{T}_{2}})}{l}dt \\\ & \Rightarrow ms{{T}_{1}}-msT{{'}_{1}}=\dfrac{KA({{T}_{1}}-{{T}_{2}})}{l}dt \\\ & \Rightarrow msT{{'}_{1}}=ms{{T}_{1}}-\dfrac{KA({{T}_{1}}-{{T}_{2}})}{l}dt \\\ & \Rightarrow T{{'}_{1}}={{T}_{1}}-\dfrac{KA({{T}_{1}}-{{T}_{2}})}{msl}dt\text{ }.....................\text{(ii)} \\\ \end{aligned}$$ Here $$T{{'}_{1}}$$gives us the fall in temperature of the water in vessel 1. As there is heat loss, there will be heat gain also which will here take place by the water in vessel 2. Heat gain by a substance is given as $$dQ=ms({{T}_{f}}-{{T}_{i}})$$ Where m is mass of the substance, s is specific heat of substance, $${{T}_{i}}$$is the initial temperature of the substance and $${{T}_{f}}$$is the final temperature. Now heat gain by the water in vessel 2, if $${{T}_{2}}$$is initial temperature and $$T{{'}_{2}}$$is final temperature for the water in vessel 2 whereas the mass of water will be m and specific heat is s, then $$dQ=ms(T{{'}_{2}}-{{T}_{2}})$$ Again using equation (i) we get $$\begin{aligned} & ms(T{{'}_{2}}-{{T}_{2}})=\dfrac{KA({{T}_{1}}-{{T}_{2}})}{l}dt \\\ & \Rightarrow msT{{'}_{2}}-ms{{T}_{2}}=\dfrac{KA({{T}_{1}}-{{T}_{2}})}{l}dt \\\ & \Rightarrow msT{{'}_{2}}=ms{{T}_{2}}+\dfrac{KA({{T}_{1}}-{{T}_{2}})}{l}dt \\\ & \Rightarrow T{{'}_{2}}={{T}_{2}}+\dfrac{KA({{T}_{1}}-{{T}_{2}})}{msl}dt\text{ }......................\text{(iii)} \\\ \end{aligned}$$ Here $$T{{'}_{2}}$$gives us the rise in temperature of the water in vessel 2. Now subtracting equation (iii) from (ii) we get $$\begin{aligned} & T{{'}_{1}}-T{{'}_{2}}=\left( {{T}_{1}}-\dfrac{KA({{T}_{1}}-{{T}_{2}})}{msl}dt \right)-\left( {{T}_{2}}+\dfrac{KA({{T}_{1}}-{{T}_{2}})}{msl}dt \right) \\\ & \Rightarrow T{{'}_{1}}-T{{'}_{2}}={{T}_{1}}-\dfrac{KA({{T}_{1}}-{{T}_{2}})}{msl}dt-{{T}_{2}}-\dfrac{KA({{T}_{1}}-{{T}_{2}})}{msl}dt \\\ & \Rightarrow T{{'}_{1}}-T{{'}_{2}}=\left( {{T}_{1}}-{{T}_{2}} \right)-2\dfrac{KA({{T}_{1}}-{{T}_{2}})}{msl}dt \\\ & \Rightarrow \left( {{T}_{1}}-{{T}_{2}} \right)-\left( T{{'}_{1}}-T{{'}_{2}} \right)=2\dfrac{KA({{T}_{1}}-{{T}_{2}})}{msl}dt \\\ & \Rightarrow dT=2\dfrac{KA({{T}_{1}}-{{T}_{2}})}{msl}dt \\\ & \Rightarrow \dfrac{dT}{({{T}_{1}}-{{T}_{2}})}=\dfrac{2KA}{msl}dt \\\ \end{aligned}$$ dT is the total change in temperature of the system. Integrating the above equation where upper limit for dT will be $$\dfrac{{{T}_{1}}-{{T}_{2}}}{2}$$and lower limit for dT will be $${{T}_{1}}-{{T}_{2}}$$ and for dt limit will be from 0 to t. Hence taking these limit and integrating we get $$\begin{aligned} & \int\limits_{{{T}_{1}}-{{T}_{2}}}^{\dfrac{{{T}_{1}}-{{T}_{2}}}{2}}{\dfrac{dT}{({{T}_{1}}-{{T}_{2}})}=\int\limits_{0}^{t}{\dfrac{2KA}{msl}dt}} \\\ & \Rightarrow \left[ \ln ({{T}_{1}}-{{T}_{2}}) \right]_{{{T}_{1}}-{{T}_{2}}}^{\dfrac{{{T}_{1}}-{{T}_{2}}}{2}}=\dfrac{2KA}{msl}\left[ t \right]_{0}^{t} \\\ & \Rightarrow \left[ \ln \dfrac{({{T}_{1}}-{{T}_{2}})}{2}-\ln ({{T}_{1}}-{{T}_{2}}) \right]=\dfrac{2KA}{l}\left[ t-0 \right] \\\ & \Rightarrow \ln \dfrac{\dfrac{({{T}_{1}}-{{T}_{2}})}{2}}{({{T}_{1}}-{{T}_{2}})}=\dfrac{2KA}{l}t \\\ & \Rightarrow \ln \dfrac{1}{2}=\dfrac{2KA}{l}t \\\ & \Rightarrow t=\dfrac{l}{2KA}\ln \dfrac{1}{2} \\\ \end{aligned}$$ **Note:** Here the upper limit of dT is the final temperature difference between the water in the vessel 1 and 2 Whereas the lower limit is the initial temperature difference. As we had to find the time when the temperature difference reduced by half of the original value so the final temperature difference was taken $$\dfrac{({{T}_{1}}-{{T}_{2}})}{2}$$.