Question
Question: Figure shows the x-t plot of 1-D motion of a particle. Is it correct to say from the graph that the ...
Figure shows the x-t plot of 1-D motion of a particle. Is it correct to say from the graph that the particle moves in a straight line for t < 0 and on a parabolic path for t > 0? If not, suggest a suitable physical context for this graph.
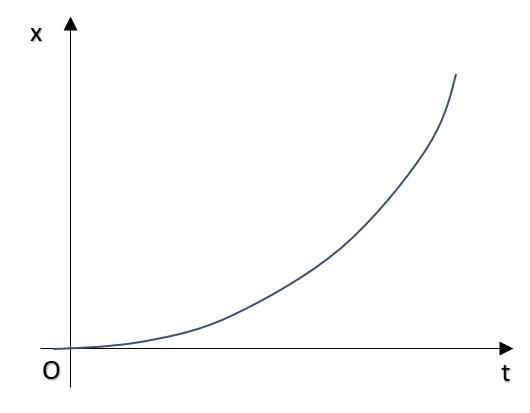
Solution
Considering only the motion of particles due to natural parameters like gravity, any motion on earth could be divided into two categories. straight line and parabolic path. A motion is parabolic if the initial velocity is not in the direction of acceleration due to gravity. Whereas a motion is a straight line only if either the velocity is zero or is in or opposite to the direction of acceleration due to gravity.
Complete step by step answer:
Since we’ve been asked about physical context, we can suggest the motion or situation related to daily life problems. We have to think about a scenario where displacement and time varies in parabolic form.
Let’s consider the free fall motion of a body. During free fall, we have acceleration of the body to be constant. Let’s see what will be the relation between displacement (x) and time (t).
We have a=g
As a=dtdv
Hence g=dtdv
⟹dv=gdt
Integrating both sides, we get;
∫dv=∫gdt
⟹v=g∫dt
⟹v=gt+c
Now, we have considered free fall of the body, which means at t=0, v=0
Thus applying this condition, we get;
0=g(0)+c
⟹c=0
Hence we have v=gt
Now, as v=dtdx
Thus, dtdx=gt
⟹dx=gtdt
Integrating, we get
∫dx=∫gtdt
⟹x=g∫tdt=g2t2
Hence we get, x=2gt2
Hence, we can see that if the body undergoes a constant acceleration, its path is parabolic with time.
But saying that it moves in a parabolic path won’t be correct. For that we have to establish an equation between ‘x’ and ‘y’ coordinates. As it is mentioned that it is free fall, means it doesn’t have any velocity in any direction. Hence the path will be straight line, not parabolic.
Note: By seeing the x-t graph, we cannot say anything about the motion of particles. Before t =0, the displacement of the body was not changing with time which suggests that the body is at rest. After t=0, the body started moving with a constant acceleration.
