Question
Question: Figure shows the variation of frequency of a characteristic X-ray and atomic number....
Figure shows the variation of frequency of a characteristic X-ray and atomic number.
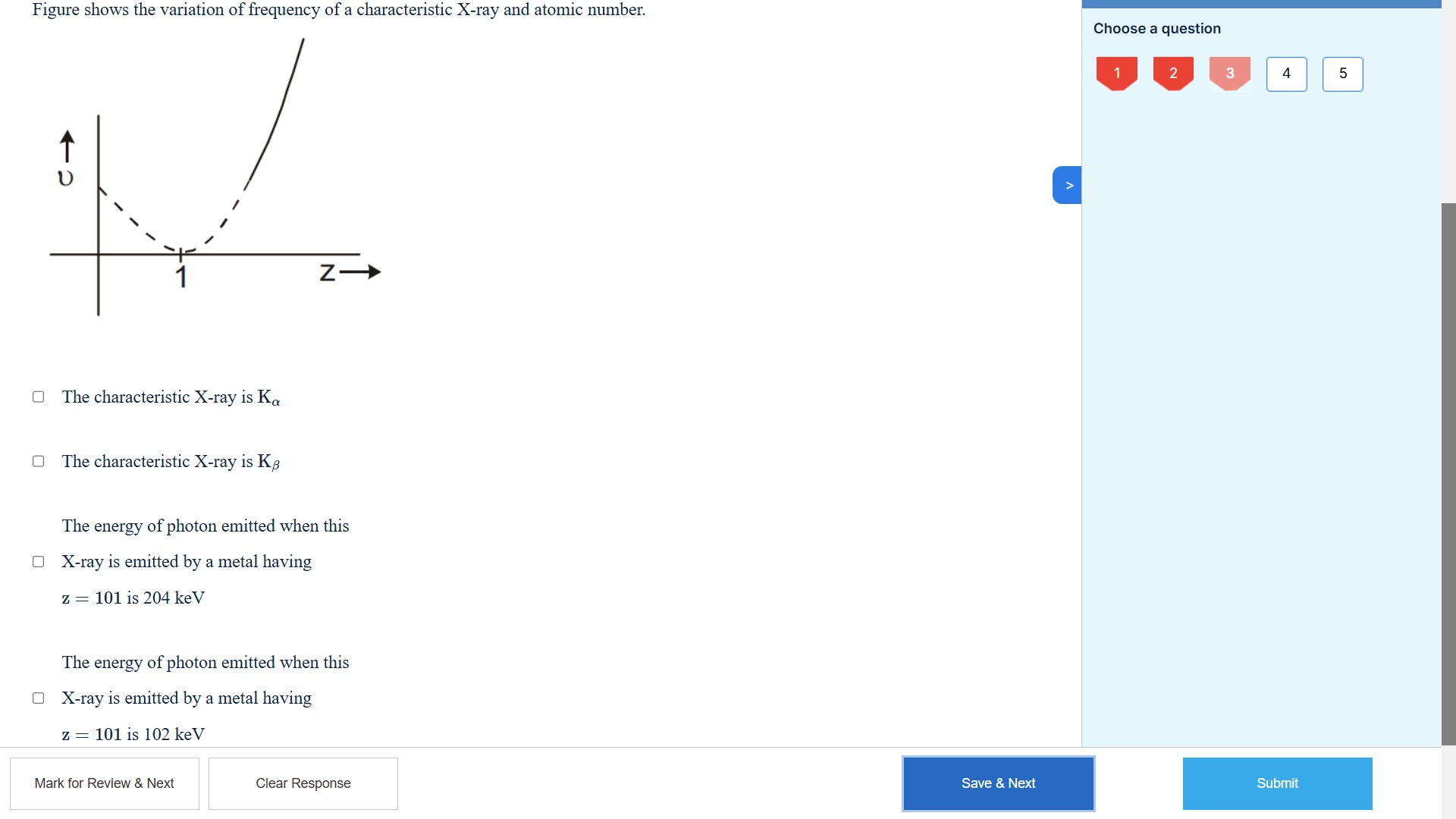
The characteristic X-ray is Kα
The characteristic X-ray is Kβ
The energy of photon emitted when this X-ray is emitted by a metal having z = 101 is 204 keV
The energy of photon emitted when this X-ray is emitted by a metal having z = 101 is 102 keV
The characteristic X-ray is Kα, The energy of photon emitted when this X-ray is emitted by a metal having z = 101 is 102 keV
Solution
The graph shows the variation of frequency ν of a characteristic X-ray with atomic number Z. According to Moseley's law, for a characteristic X-ray of a given series, the frequency is related to the atomic number by ν=a(Z−b), where a and b are constants. Thus, ν=a2(Z−b)2. For K-series X-rays, the screening constant b is approximately 1. The graph shows that ν≈0 when Z=1, which is consistent with b=1. So we can write ν=A(Z−1)2 for some constant A.
The energy of the emitted photon is E=hν=hA(Z−1)2. Let E0=hA. Then E=E0(Z−1)2. The constant E0 depends on the specific transition. For the K-series, the transitions are to the K shell (n1=1).
For the Kα line, the transition is from the L shell (n2=2) to the K shell (n1=1). The energy is given by EKα=Ry(Z−1)2(121−221)=Ry(Z−1)243. So, E0=Ry43, where Ry is the Rydberg constant for energy, approximately 13.6 eV. E0≈13.6×43=10.2 eV. Thus, EKα≈10.2(Z−1)2 eV.
For the Kβ line, the transition is from the M shell (n2=3) to the K shell (n1=1). The energy is given by EKβ=Ry(Z−1)2(121−321)=Ry(Z−1)298. So, E0=Ry98. E0≈13.6×98≈12.09 eV. Thus, EKβ≈12.09(Z−1)2 eV.
Now let's evaluate the energy for Z=101. If the characteristic X-ray is Kα, EKα(Z=101)≈10.2(101−1)2=10.2×1002=10.2×10000=102000 eV = 102 keV. If the characteristic X-ray is Kβ, EKβ(Z=101)≈12.09(101−1)2=12.09×10000=120900 eV = 120.9 keV.
The calculated energy for Kα at Z=101 is 102 keV, which matches the fourth option. This suggests that the characteristic X-ray is Kα.
