Question

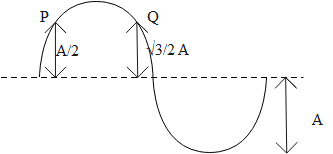
Figure shows the snapshot of the transverse sinusoidal wave on a string at $t=0$sec. The frequency of the wave is $\dfrac{125}{6}Hz$. ${{T}_{1}}$ is the time at which the line joining P and Q become horizontal for the first time after $t=0$if the wave is travelling towards +ve x-direction and ${{T}_{2}}$ is the time at which the line joining P and Q become horizontal for the first time after $t=0$if the wave is travelling towards -ve x-direction. Then the value of $\dfrac{{{T}_{1}}}{{{T}_{2}}}$ is

Answer 1

Using the phase difference formula, we will find the wavelength of the wave. Then, using the formula that relates the frequency, wavelength and time period, we will find the values of the time at which the line becomes horizontal. Finally, we will find the ratio of the same.
Formula used:
$T=\dfrac{\lambda }{\upsilon }$
$\phi =\dfrac{2\pi \times \delta }{\lambda }$

Complete answer:
From the given information, we have the data as follows.
The frequency, $f=\dfrac{125}{6}Hz$
At the time${{T}_{1}}$ , the amplitude at P and Q, $P=\dfrac{A}{2},Q=\dfrac{\sqrt{3}}{2}A$
The time taken for $f=\dfrac{125}{6}Hz$ is 1 sec.
${{T}_{1}}$ is the time at which the line joining P and Q become horizontal for the first time after $t=0$if the wave is travelling towards +ve x-direction and ${{T}_{2}}$ is the time at which the line joining P and Q become horizontal for the first time after $t=0$if the wave is travelling towards -ve x-direction.
The phase difference is,
$\phi =\dfrac{2\pi \times \delta }{\lambda }$
Where $\phi$is the phase difference, $\delta$is the path difference and $\lambda$is the wavelength.
The formula for computing the time period using the wavelength and the frequency is given as follows.
$T=\dfrac{\lambda }{\upsilon }$
The time taken at an angle of $150{}^\circ$is given as follows.
Substitute the values in the above formula.

& {{T}_{1}}=\dfrac{1}{\dfrac{125}{6}\times \dfrac{360{}^\circ }{30{}^\circ }} \\\ & \Rightarrow {{T}_{1}}=\dfrac{6\times 30}{125\times 360} \\\ & \therefore {{T}_{1}}=\dfrac{1}{250}s \\\ \end{aligned}$$ Similarly the time taken at an angle of $$150{}^\circ $$is given as follows. $$\begin{aligned} & {{T}_{2}}=\dfrac{1}{\dfrac{125}{6}\times \dfrac{360{}^\circ }{150{}^\circ }} \\\ & \Rightarrow {{T}_{2}}=\dfrac{6\times 150}{125\times 360} \\\ & \therefore {{T}_{2}}=\dfrac{1}{50}s \\\ \end{aligned}$$ Therefore, values of the time at which the line joining P and Q become horizontal for the first time after $$t=0$$if wave is travelling towards +ve x-direction and time at which the line joining P and Q become horizontal for the first time after $$t=0$$if wave is travelling towards -ve x-direction are: $${{T}_{1}}=\dfrac{1}{250}s$$ and $${{T}_{2}}=\dfrac{1}{50}s$$ Now, we will compute the ratio of these times. $$\begin{aligned} & \dfrac{{{T}_{1}}}{{{T}_{2}}}=\dfrac{{}^{1}/{}_{250}}{{}^{1}/{}_{50}} \\\ & \Rightarrow \dfrac{{{T}_{1}}}{{{T}_{2}}}=\dfrac{50}{250} \\\ & \therefore \dfrac{{{T}_{1}}}{{{T}_{2}}}=\dfrac{1}{5} \\\ \end{aligned}$$ $$\therefore $$ The ratio of the time at which the line joining P and Q become horizontal for first time after $$t=0$$if wave is travelling towards +ve and -ve x-direction is $$\dfrac{1}{5}$$. **Note:** We have used the formula that relates the phase difference, that is, an angle with the wavelength and the basic formula that relates the time period and the frequency of the wave to solve this problem.