Question
Question: Figure shows the path of a light beam in an isosceles prism with apex angle \( \delta = {60^ \circ }...
Figure shows the path of a light beam in an isosceles prism with apex angle δ=60∘ (inside the prism beam is parallel to the base). Find the angle of deflection in degrees. The refractive index of prism material is 1.732
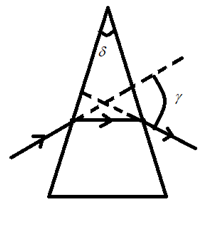
Solution
Since the light is incident on a glass prism the light refracts or produces a deviation due to the difference in the medium it is travelling in. The formula for the refractive index in terms of the sin of the angles of the prism and the minimum angle of deviation is required to be applied here in order to find out the angle of the deviation of incident light.
Complete Step By Step Answer:
The above problem revolves around the concept of refraction of light through prisms and hence the concept of angle of deviation must be known.
Refraction is the phenomenon of bending of light when light travels from one medium to another where there is a variation in the reactive index of the material. The glass medium is optically denser than air medium and hence the deviation is observed and the light tends to bend towards the normal when moving from denser to rarer medium and vice versa.
When a ray of light falls on the prism, a deviation is observed due to a difference in the medium travelled by the incident light and this angle by which it deviates is known as the angle of deviation. Hence it is imperative to calculate this angle of deviation of light. The angle of deviation is hence said to be the angle between the incident ray and the emergent ray as shown clearly in the figure. It depends on the angle of the prism, the angle of incidence and the angle of emergence.
We know that from Snell’s law that:
μ=sinrsini
Here, r the angle of refraction is the angle of emergence e and hence the formula becomes:
μ=sinesini
From the derivations for the angle of incidence and emergence for prisms we know that the angle of incidence and emergence is given by the formulae:
i=2A+δ
e=2δ
By substituting these values into the Snell’s law equation, we can now construct the equation for the refractive index in terms of the angle of deviation and the angle of the prism for the incident light on the surface of the prism. The equation is as follows:
μ=sin(2δ)sin(2A+δ) ---------( 1 )
We are already given the values of the refractive index, the apex angle which is nothing but the angle of the prism and we are required to find out the angle of deviation of the prism. Hence we have:
Given,
A=60∘
μ=3
Hence by substituting the values in equation ( 1 ) we get:
3=sin(260)sin(260+δ)
On solving further we get:
⇒3=sin(30)sin(260+δ)
Since, sin30∘=21
⇒3×21=sin(260+δ)
Taking the inverse of the sin angle on both sides we get:
⇒sin−1(23)=sin−1(sin(30+2δ))
⇒60=30+2δ
On solving further for angle of deviation we get:
⇒2δ=30
⇒δ=60∘
Hence this is the angle of deviation of the prism.
Additional Information:
A ray of light suffering refraction through a prism is bent towards the base of the prism. The deviation produced by a prism is maximum when the angle of incidence is 90∘ . When a ray of light is refracted through a prism, the sum of the angle of incidence and the angle of emergence is equal to the sum of the angle of the prism and the angle of deviation.
The factors on which the angle of deviation depends on is the material of the prism, angle of incidence, the wavelength of light used and the angle of the prism.
Note:
The common misconception is that the angle is supposed to be calculated from the normal, that is the angle deviated from the normal is said to be the angle of the incident light on the prism. The formula for angle of deviation with respect to the refractive index formula in terms of the sin angle needs to be applied here rather than the common formula which is a point to be noted.
