Question

Figure shows the P-V plot of an ideal gas taken through a cycle ABCDA. The Part ABC is a semi circle and CDA is a half of an ellipse then.

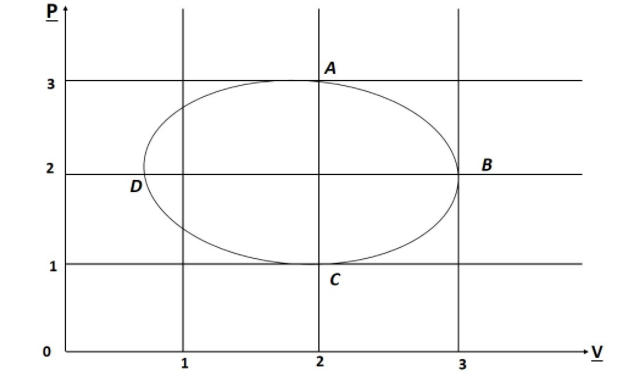
A. the Process during the Path A ⟶ B is isothermal
B. heat flows out of the gas during the Path B ⟶C ⟶ D
C. Work done during the path A ⟶B ⟶ C is zero
D. Positive work is done by the gas in the Cycle ABCDA.
This question has Multiple Correct options:

Answer 1

Hint Work done needed to be Converted into Single variable. Other than this, isothermal Process is when the temperature doesn’t change i.e., $\Delta {\rm{T}} = 0$ and if work done is negative the Work is done on the Work is done by the gas and it releases out.
Let’s begin with the option D, the work done by the fig path ABCDA will be Positive not, the Pressure, Volume and Temperature remains Same no changes occurred finally. The Work done in the PV graph is Calculated by the total area Covered by the figure.
As we can see, the area Covered here is half of area Circle and half of area of eclipse.
$\therefore {\rm{Work\;done}} = \dfrac{{{\rm{\pi }}{{\left( {\dfrac{{3 - 1}}{2}} \right)}^2}}}{2} + \dfrac{{{\rm{\pi }}\left( {2 - 1.5} \right)\left( {3 - 1} \right)}}{2}$
$= \dfrac{{\rm{\pi }}}{2} + \dfrac{{\rm{\pi }}}{2} = {\rm{\pi }} = 3.14$
Thus option D is Correct.
Now, lets get to option C, Work done in Path A ⟶ B ⟶C is zero or not.
as ABC is a Semicircle of radius 1, we know that, the work done is area Under the PV graph
For A ⟶ B
$\Delta {{\rm{V}}_{{\rm{AB}}}} = - {\rm{ve}}$, So work done is also –ve $\Delta {{\rm{W}}_{{\rm{AB}}}} = - {\rm{ve}}$.
For B ⟶ C
$\Delta {{\rm{V}}_{{\rm{BC}}}} = + {\rm{ve}}$, So the Work done is +ve $\Delta {{\rm{W}}_{{\rm{BC}}}} = + {\rm{ve}}$
Also we know that $\left| {{{\rm{W}}_{{\rm{AB}}}}} \right| > \left| {{{\rm{W}}_{{\rm{BC}}}}} \right|$ Hence the total work done is not zero.
Therefore option C is incorrect.
Now, get to the option B is correct or not. The option says the flows out of the gas during Path B ⟶ C ⟶D.
As we know the first law of thermodynamics
$\Delta {\rm{V}} = {\rm{Q}} - {\rm{W}}$, Where Q is the Sum of all heat transfer into and out of the System.
if Q is negative heat flows out of the gas and if Q is positive heat flows in the gas i.e., System.
As we can see in the graph, the Volume as well as the temperature reduces out, thus It leads to ∆V negative.
Hence this leads to the Q being negative and heat flowing out of the gas.
Option no B is Correct.
Now, approach towards option no A. It says that Process A ⟶ B is Isothermal.
To check if the Process is Isothermal or not, the Condition required is $\Delta {\rm{T}} = 0$.
If there is no change is Temperature, in the entire Process, then the Ideal gas law gives out ${\rm{PV}} = {\rm{Constant}}$ as a graphical form of hyperbola. But the given Path as A ⟶ B follows the circular Path ${{\rm{P}}^2} + {{\rm{V}}^2} = {\rm{Constant}}$, where there is change in Temperature.
Hence, option D is incorrect.

So, the correct options are B and D

Note Try to check each and every option with Assumption of being right and prove it. Always check total work done with their magnitude Sign, where eventually 2 work down might Cancel each other.