Question

Figure shows the graph of association of particles as a function of time. The maximum speed of the particles is (particle starts from rest)-

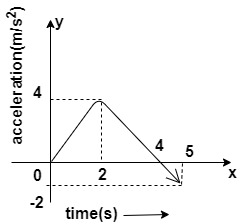
(A) 7m/s
(B) 8m/s
(C) 4m/s
(D) 16m/s

Answer 1

Hint : Acceleration is defined as: The rate of change of velocity with respect to time. Acceleration is a vector quantity as it has both magnitude and direction. It is also the second derivative of position with respect to time. OR It is the first derivative of velocity with respect to time.
Acceleration (a) $=~\text{dv}/\text{dt}$

Complete step by step solution:
We have given, A graph of acceleration of particles as a function of time. We have to calculate the maximum speed of particles. Acceleration is defined as the rate of change of velocity with respect to time.
$\text{a}=~\text{dv}/\text{dt}$
$\text{dv}=\text{a}\times \text{dt}$
Taking integration on both sides
$\int{dv}=a\int{dt}$ ------ (1)
Limit of integration Since, particle starts from rest (v=0) and, let maximum velocity is V and initial time is t = 0 and Time at which acceleration is maximum t = 2
i.e. $\text{V}\to \text{0}$ to V
$\text{t}\to \text{0}$ to 2
From eq. (1)
$\int\limits_{0}^{V}{dv}=a\int\limits_{0}^{2}{dt}$
Acceleration is given by, a = 4
$\left[ v \right]_{0}^{V}=4\left[ t \right]_{0}^{2}$
$v-0=4\left[ 2-0 \right]$
$V=8m{{s}^{-1}}$
Hence, maximum velocity is $8ms^{-1}$ .

Note:
Another method : Acceleration is given by
$a=\dfrac{change\text{ }in\text{ }velocity}{time\text{ }taken}$
$a=\dfrac{{{v}_{2}}-{{v}_{1}}}{{{t}_{2}}-{{t}_{1}}}$
From graph, (figure)
a = 4m/s2
$\begin{aligned} & {{v}_{2}}=Vm/s \\\ & {{v}_{1}}=0 \\\ & {{t}_{2}}=2,{{t}_{1}}=0 \\\ & 4=\dfrac{V-0}{2-0} \\\ & V=8m/s \\\ \end{aligned}$
This is the maximum velocity /speed of a particle.