Solveeit Logo
Login

Question

Question: Figure shows part of a circuit. If \(I{\text{ }} = {\text{ }}7{\text{ }}A\) and is decreasing at a c...

Figure shows part of a circuit. If I = 7 AI{\text{ }} = {\text{ }}7{\text{ }}A and is decreasing at a constant rate of 500 A/s500{\text{ }}A/s, then VB − VA{V_B}{\text{ }} - {\text{ }}{V_A} is

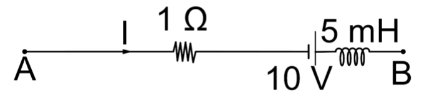
A. − 1.5 V - {\text{ }}1.5{\text{ }}V
B. 2.5 V2.5{\text{ }}V
C. − 3.5 V - {\text{ }}3.5{\text{ }}V
D. 5.5 V5.5{\text{ }}V

Explanation

Solution

We will directly form an equation as we move from A to B using the conventions of Kirchhoff’s rule. Then, we will substitute the appropriate values and then evaluate the required solution.

Complete step by step answer:
Firstly we start from point A and we start the equation with VA{V_A}. Then, we move to the resistor and we observe that we are moving with the current in the resistor and thus we will have a potential drop thus, we proceed with VA − IR{V_A}{\text{ }} - {\text{ }}IR.

Now, we reach the cell and we are moving from the negative to the positive end which means we are moving from a point of lower potential to a point of higher potential and thus, we will have a potential lift.Thus, we get
VA − IR + V{V_A}{\text{ }} - {\text{ }}IR{\text{ }} + {\text{ }}V
Then, we reach the inductor and we move along with the current and thus there is a potential drop.Thus, we get
VA − IR + V + L dIdt{V_A}{\text{ }} - {\text{ }}IR{\text{ }} + {\text{ }}V{\text{ }} + {\text{ }}L{\text{ }}\dfrac{{dI}}{{dt}}
Finally, we reach the final point B. Thus, we get
VA − IR + V + L dIdt = VB{V_A}{\text{ }} - {\text{ }}IR{\text{ }} + {\text{ }}V{\text{ }} + {\text{ }}L{\text{ }}\dfrac{{dI}}{{dt}}{\text{ }} = {\text{ }}{V_B}

Further, we rearrange the equation and we get
VB − VA = V + L dIdt − IR −−−−−−− (i){V_B}{\text{ }} - {\text{ }}{V_A}{\text{ }} = {\text{ }}V{\text{ }} + {\text{ }}L{\text{ }}\dfrac{{dI}}{{dt}}{\text{ }} - {\text{ }}IR{\text{ }} - - - - - - - {\text{ }}(i)
Now, we will observe the given values
V = 10 VV{\text{ }} = {\text{ }}10{\text{ }}V
⇒R = 1 Ω\Rightarrow R{\text{ }} = {\text{ }}1{\text{ }}\Omega
⇒I = 7 A\Rightarrow I{\text{ }} = {\text{ }}7{\text{ }}A
As an inductor opposes the flowing current.
Thus, the value of inductance will be negative.
L = − 5 mH = − 5 × 10−3 HL{\text{ }} = {\text{ }} - {\text{ }}5{\text{ }}mH{\text{ }} = {\text{ }} - {\text{ }}5{\text{ }} \times {\text{ }}{10^{ - 3}}{\text{ }}H
Since, there is a current decay in the inductor. Thus, the value of dIdt\dfrac{{dI}}{{dt}} is negative.Thus,
dIdt = − 5 × 102 A/s\dfrac{{dI}}{{dt}}{\text{ }} = {\text{ }} - {\text{ }}5{\text{ }} \times {\text{ }}{10^2}{\text{ }}A/s

Substituting these values in equation (i)(i), we get
VB − VA = 10 + (5 × 10−3) × (5 × 102) − 7 × 1{V_B}{\text{ }} - {\text{ }}{V_A}{\text{ }} = {\text{ }}10{\text{ }} + {\text{ }}\left( {5{\text{ }} \times {\text{ }}{{10}^{ - 3}}} \right){\text{ }} \times {\text{ }}\left( {5{\text{ }} \times {\text{ }}{{10}^2}} \right){\text{ }} - {\text{ }}7{\text{ }} \times {\text{ }}1
Further, we get
VB − VA = 10 + 25 × 10−1 − 7{V_B}{\text{ }} - {\text{ }}{V_A}{\text{ }} = {\text{ }}10{\text{ }} + {\text{ }}25{\text{ }} \times {\text{ }}{10^{ - 1}}{\text{ }} - {\text{ }}7
Then, we get
VB − VA = 3 + 2.5{V_B}{\text{ }} - {\text{ }}{V_A}{\text{ }} = {\text{ }}3{\text{ }} + {\text{ }}2.5
Finally, we get
∴VB − VA = 5.5 V\therefore {V_B}{\text{ }} - {\text{ }}{V_A}{\text{ }} = {\text{ }}5.5{\text{ }}V

Hence, the correct answer is D.

Note: Students should be very cautious while using the values of inductance and current decay. Students should use the idea of exponents as otherwise, they will arrive into a situation of clumsy calculations.