Question

Figure shows inverted T shaped fixed pipe. Liquid is released from rest from the position shown. Liquid is non-viscous.

(A) Velocity of fluid particle in vertical part of tube when level of liquid in it remains H/2 will be $\sqrt{\frac{3gH}{8}}$

(B) The initial acceleration of the fluid particle in vertical tube will be g/2

(C) Initial gauge pressure at point P will be $\rho gH/4$

(D) None of the above

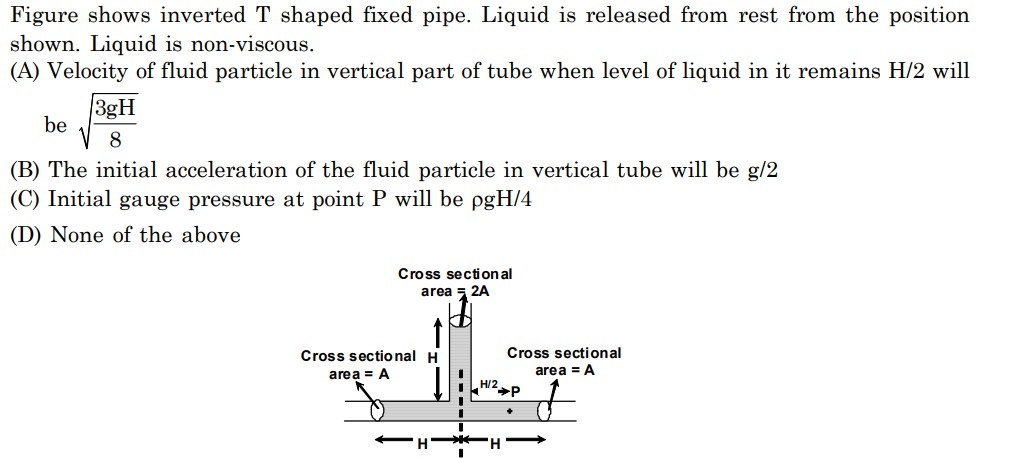
• A. Velocity of fluid particle in vertical part of tube when level of liquid in it remains H/2 will be $\sqrt{\frac{3gH}{8}}$
• B. The initial acceleration of the fluid particle in vertical tube will be g/2
• C. Initial gauge pressure at point P will be $\rho gH/4$
• D. None of the above

Answer 1

Answer: (A), (B), (C)

(A), (B) and (C) are correct.

Answer 2

Solution Explanation:

A short outline of the reasoning is as follows. One may analyze the initially perturbed motion of the liquid in the closed “inverted‐T” pipe by applying unsteady Bernoulli’s equation and the momentum–energy methods. In the problem the fluid in the vertical part (cross‐section 2A) and in the horizontal parts (each with cross‐section A) are coupled by continuity. When the free level in the vertical tube reaches H/2, an energy–balance analysis shows that the kinetic energy accumulated is such that the speed in the vertical tube becomes

  v = √(3gH/8).

Similarly, a force–balance (or applying Euler’s equation along a streamline) shows that the effective acceleration initially is only g/2 rather than g. Finally, taking the reduced effective gravity (g – a = g/2) over the vertical height H/2 between the free surface and point P (which is H/2 horizontally away from the vertical branch, and on the same horizontal level) gives a corresponding initial gauge pressure of

  p_g = ρ·(g/2)·(H/2) = ρgH/4.

Thus all three statements (A), (B) and (C) are found to be correct.