Question
Question: Figure shows grouping of identical cells each of emf \(4V\) and internal resistance \(1\Omega \). Th...
Figure shows grouping of identical cells each of emf 4V and internal resistance 1Ω. This combination can be replaced by an equivalent cell between A and B having emf E and internal resistance r, where
(A). E=72V,r=18Ω
(B). E=24V,r=18Ω
(C). E=72V,r=2Ω
(D). E=24V,r=2Ω
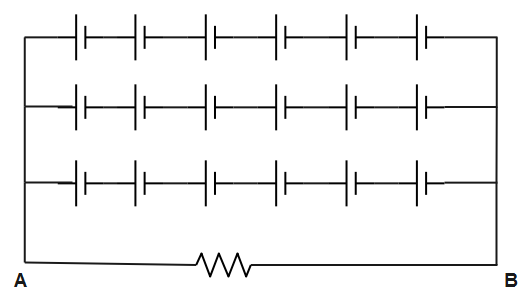
Solution
Figure shows batteries connected in series and parallel combination. The combination of batteries is similar to the combination of resistances. Therefore, using formula for equivalent emf in series and equivalent resistances in series we can get a combination of batteries purely in parallel combination, we can solve the combination to calculate the equivalent emf and internal resistance in the circuit.
Formulas used:
Eeq=E1+E2+E3+−−+En
req=r1+r2+r3+−−+rn
req1=r11+r21+r31+−−+rn1
Complete answer:
For all elements connected in series, the current passing through them is the same while for all elements connected in parallel the potential drop is the same. Batteries can also be connected in series or parallel combination.
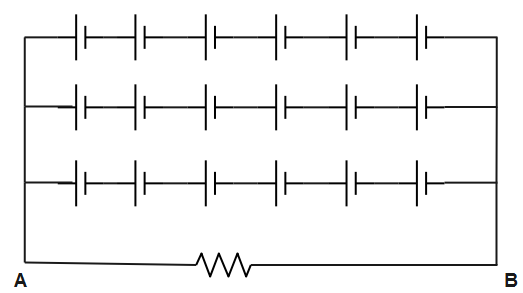
In the above figure, given that each battery has emf 4V and their internal resistance is 1Ω.
For series combination of batteries, the equivalent emf is given by-
Eeq=E1+E2+E3+−−+En
Similarly the equivalent internal resistance of batteries connected in series will be-
req=r1+r2+r3+−−+rn
The equivalent emf of batteries connected in series in the figure will be-
Eeq=4×6=24V
The equivalent resistance of batteries connected in series will be-
req=1×6=6Ω
Therefore, the equivalent resistance of batteries connected in series is 24V and internal resistance is 6Ω. Hence, the above circuit will be simplified as-
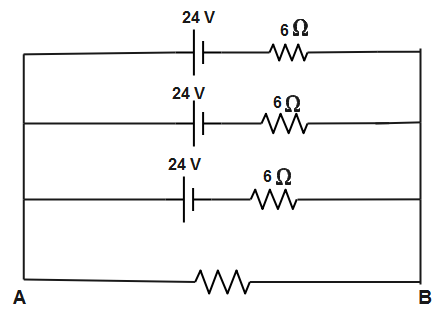
For all batteries connected in parallel, as the voltage is same in parallel, the equivalent emf will be 24V.
For internal resistances connected in parallel, the formula for equivalent internal resistances is-
req1=r11+r21+r31+−−+rn1
Therefore, the equivalent internal resistance will be-
r1=61+61+61⇒r1=63∴r=2Ω
Therefore, the equivalent internal resistance will be 2Ω.
Therefore, the combination of batteries can be replaced by a battery of emf 24V having internal resistance 2Ω.
Hence, the correct option is (D).
Note:
The emf is the potential developed by a battery. It is always greater than the potential difference. Potential difference is the difference of electric potential between two points in a circuit. Charge always flows from a point of high potential to a point of low potential. Flow of charge is called current.
