Question

Figure shows graph between I and V for two conductors A and B. Their respective resistances are in the ratio.

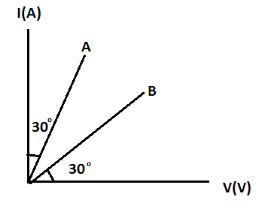
A. 1:1
B. 1:3
C. 3:1
D. 1:2

Answer 1

We will first use the Ohm’s law which provides the relationship between the current and voltage across the circuit along with the proportionality constant resistance. We will use the relationship to find the slope of the two conductors A and B finding the relationship between the two resistances using the two slopes.

Complete step by step answer:
According to Ohm's law, “Under a definite physical condition, the current flowing through the conductor is directly proportional to the applied potential difference at its ends. Thus,

$$I \propto V \\\ \Rightarrow V = IR$$

And here, R is the proportionality constant, which is called the resistance of the conductor. Resistance of a conductor is the ability of a conductor to resist the flow of electrons in the conductor, which is how much it stops current to get flowing in the conductor.
In our case, the ratio of current and voltage gives slope which is the tangential angle.

\Rightarrow\dfrac{I}{V} = \tan \theta \\\ \Rightarrow\dfrac{I}{V} = m$$ Now, for the variation of A, which is change in voltage with respect to change in current, we have the angle with the X-axis $$\theta = 60^\circ = {m_A} = \tan 60^\circ = \sqrt 3 $$ Thus;

\dfrac{1}{{{R_A}}} = \sqrt 3 \\
\Rightarrow {R_A} = \dfrac{1}{{\sqrt 3 }}

Now, for the variation of B, we have the angle with the X-axis, $$\theta = 30^\circ = {m_B} = \tan 30^\circ = \dfrac{1}{{\sqrt 3 }}$$ Thus we have here;

\dfrac{1}{{{R_B}}} = \dfrac{1}{{\sqrt 3 }} \\
\therefore {R_B} = \sqrt 3

Thus the ratio of resistances is given as ${R_A}:{R_B}=1:3$ **Thus, option B is the correct answer.** **Note:** The slope of any line on the two dimensional plane can be given by the value of $$\tan \theta $$ where $$\theta $$ is the angle of the line with the X-axis. Hence, $$\tan \theta $$ is the value of the ratio of the value of the Y-axis and the X-axis at a particular point on the line. The linear relationship of Ohm’s law is only valid for metallic materials.