Question

Figure shows four Gaussian surfaces consisting of identical cylindrical midsections but different end caps. The surfaces are in a uniform electric field that is directed parallel to the central axis of each cylindrical midsection. The end caps have these shapes: $S_1$, convex hemispheres; $S_2$, concave hemispheres; $S_3$, cones; $S_4$, flat disks. Mark the correct statement(s).

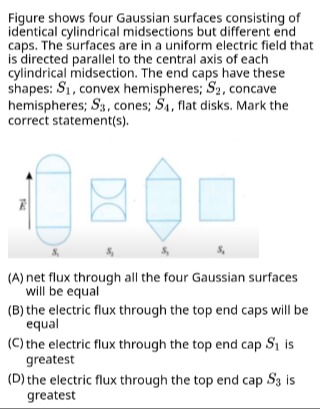
• A. net flux through all the four Gaussian surfaces will be equal
• B. the electric flux through the top end caps will be equal
• C. the electric flux through the top end cap $S_1$ is greatest
• D. the electric flux through the top end cap $S_3$ is greatest

Answer 1

Answer: (A), (B)

A, B

Answer 2

The problem describes four different Gaussian surfaces ($S_1, S_2, S_3, S_4$) in a uniform electric field ($\vec{E}$). All surfaces have identical cylindrical midsections, but their end caps differ. The electric field is directed parallel to the central axis of each cylindrical midsection.

Understanding Electric Flux and Gauss's Law:

1. Electric Flux ($\Phi$): For a surface, it's defined as $\Phi = \int \vec{E} \cdot d\vec{A}$. In a uniform electric field, the flux through an open surface can be calculated as $\Phi = E A_{proj}$, where $A_{proj}$ is the area of the projection of the surface onto a plane perpendicular to the electric field.

2. Gauss's Law: For any closed surface, the net electric flux through it is given by $\Phi_{net} = \frac{Q_{enc}}{\epsilon_0}$, where $Q_{enc}$ is the net charge enclosed by the surface.

Analysis of Statement (A): net flux through all the four Gaussian surfaces will be equal.

• The problem states that the surfaces are in a uniform electric field.

• Crucially, in a region of uniform electric field, there are no net charges enclosed within any arbitrary closed surface.

• Therefore, for all four Gaussian surfaces, the net charge enclosed ($Q_{enc}$) is zero.

• According to Gauss's Law, $\Phi_{net} = \frac{0}{\epsilon_0} = 0$.

• Thus, the net electric flux through all four Gaussian surfaces ($S_1, S_2, S_3, S_4$) will be zero. Since they are all zero, they are equal.

• Statement (A) is correct.

Analysis of Statement (B): the electric flux through the top end caps will be equal.

• The electric field $\vec{E}$ is directed parallel to the central axis of the cylindrical midsection (let's assume upwards).

• Consider any of the Gaussian surfaces. The total flux through the closed surface is $\Phi_{net} = \Phi_{top} + \Phi_{bottom} + \Phi_{cylindrical\_midsection}$.

• As established for (A), $\Phi_{net} = 0$ for all surfaces.

• For the cylindrical midsection, the electric field $\vec{E}$ is parallel to the axis, meaning it is perpendicular to the area vector $d\vec{A}$ of the curved surface. Therefore, $\vec{E} \cdot d\vec{A} = E dA \cos(90^\circ) = 0$. So, the flux through the cylindrical midsection ($\Phi_{cylindrical\_midsection}$) is zero for all four surfaces.

• This implies $0 = \Phi_{top} + \Phi_{bottom} + 0$, or $\Phi_{top} = -\Phi_{bottom}$. The magnitude of flux through the top cap is equal to the magnitude of flux through the bottom cap.

• Now, let's consider the flux through the top end caps specifically. The electric field is uniform and directed upwards.

• The flux through an open surface in a uniform electric field is given by $\Phi = E A_{proj}$, where $A_{proj}$ is the area of the projection of the surface onto a plane perpendicular to the electric field.

• All four Gaussian surfaces have identical cylindrical midsections. This means they all have the same radius, say $R$.

• Regardless of the specific shape of the top end cap (convex hemisphere, concave hemisphere, cone, or flat disk), each top end cap effectively covers a circular opening of radius $R$ at the top of the cylindrical midsection.

• The projection of each top end cap onto a plane perpendicular to the electric field (e.g., a horizontal plane) will be a disk of radius $R$.

• The area of this projected disk is $A_{proj} = \pi R^2$.

• Since $E$ is uniform and $R$ is the same for all cylindrical midsections, the electric flux through each top end cap will be $\Phi_{top} = E (\pi R^2)$.

• Therefore, the electric flux through all the top end caps will be equal.

• Statement (B) is correct.

Analysis of Statement (C) and (D): the electric flux through the top end cap $S_1$ is greatest / the electric flux through the top end cap $S_3$ is greatest.

• Since we concluded that the electric flux through all top end caps is equal (from the analysis of Statement B), it is impossible for the flux through $S_1$ or $S_3$ to be "greatest".

• Statements (C) and (D) are incorrect.

Conclusion: Both statements (A) and (B) are correct.