Question
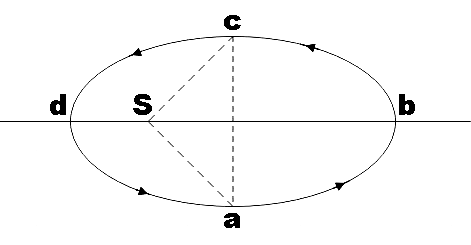
Question: Figure shows elliptical path \(abcd\) of a planet around the sun such that the area of triangle \(cs...
Figure shows elliptical path abcd of a planet around the sun such that the area of triangle csa is 41 the area of the ellipse (see figure). With db as the semi-major axis, and ca as the semi minor axis, if t1 is the time taken for planet to go over path abc and t2 for path taken over cda, then,
A. t1=4t2
B.t1=2t2
C.t1=3t2
D.t1=t2
Solution
As a first step you could recall Kepler’s second law of planetary motion. Now you could find the area swept by the planet for traveling from a to c through b and the area swept by the planet when it moves from c to a through d. Then by applying the law, you will get the required relation between the time periods.
Complete step by step answer:
Figure shows elliptical path abcd of a planet around the sun such that the area of triangle csa is 41 the area of the ellipse (see figure). With db as the semi-major axis, and ca as the semi minor axis, if t1 is the time taken for planet to go over path abc and t2 for path taken over cda, then,
In the question, we are given an elliptical path abcd of some planet around the sun such that the area of the triangle csa marked in the given figure is one-fourth the whole area of the ellipse. We are asked to find the time taken to cover cda in terms of time taken to cover the path abc.
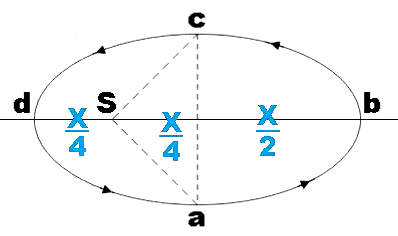
Let the total area of the ellipse be X, then the area of the triangle marked in the given figure will be, 4x
We have a semi-ellipse abc, whose area will be 2X and in the left half, the area excluding the triangle part will be, 4X
Now, let us recall Kepler’s second law. This law states that the imaginary line connecting a planet and the sun sweeps out equal areas in equal interval of time or simply, areal velocity of the planet around the sun is a constant, that is,
vA=tA=k
⇒t1A1=t2A2 ………………………. (1)
From the figure, A1 is the area swept by the planet traveling from a to c through b and A2 is the area swept by the planet when it moves from c to a through d.
A2=4X …………………………………… (2)
A1=2X+4X=43X ………………………… (3)
Substituting (2) and (3) in (1), we get,
t1(43X)=t2(4X)
⇒t13=t21
∴t1=3t2
Therefore, we found the required relation to be t1=3t2.
So, the correct answer is “Option C”.
Note: Other than the law used in solving this question, we have two other Kepler’s laws for planetary motion. The first law is called the law of elliptical orbit which states that every planet moves around in an elliptical orbit with the sun at one of its focus. Then the other law is called the law of harmonics which states that the square of the time period of a planet is directly proportional to the cube of its orbital radius.
