Question

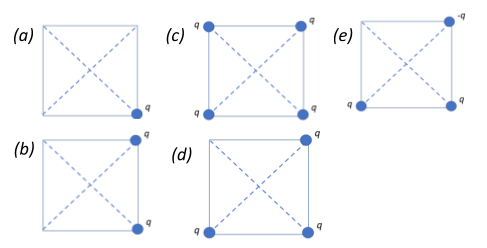
Figure shows charged beads with charges as shown in figure. The charges are placed upon the corners of a square. Rank the magnitude of the electric field at the centre in decreasing order.

Answer 1

Recall that electric field lines are always directed away from positive charges and towards the negative charges. Use this to determine the direction of the electric field(s) due to individual charges and once that is mapped out, obtain the resultant magnitude of the electric field in each case taking into account the nullifying effects of equal and opposite charges, as well as the additive nature of the charges and subsequently their vectorial field superpositions. To this end, arrange each of the cases in decreasing order of electric field magnitude.

Formula Used:
Electric field $E=\dfrac{kq}{r^2}$
$E_{resultant} = \sqrt{E_1^2+E_2^2+2E_1E_2cos\theta}$

Complete Step-by-Step Solution:
We are given five different cases in which charges are differently placed. The first four cases deal with identical charges whereas the last case includes a negative charge. We are required to find the magnitude of the electric field at the centre of each square by virtue of the presence of charges as shown accordingly.

Let the magnitude of the electric field due to a charge q at a distance r qualitatively be $E=\dfrac{kq}{r^2}$. Let r be the distance to the centre in our cases.

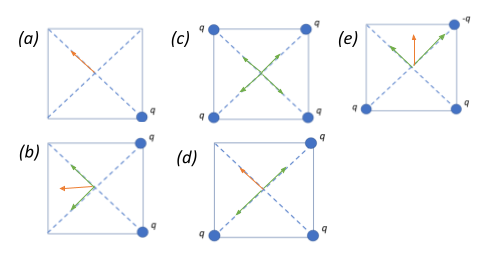
Case (a): Since there is only one charge at a corner, it exerts an electric field with a magnitude E directed as shown in the diagram since field lines are always directed away from the positive charge.
$E_{resultant} = E$

Case (b): Here we see that two identical positive charges are placed adjacent to each other in the corners of one side of the square. In such a case, we see that the electric field at the centre is a resultant of the field exerted by the two charges in the direction as shown in the diagram. Notice that they are normal to each other, as in $\theta = 90^{\circ} \Rightarrow cos90^{\circ} = 0$, and have the same magnitude,
$E_{resultant} = \sqrt{E_1^2+E_2^2+2E_1E_2cos\theta} = \sqrt{E^2+E^2+2E^2(0)} = \sqrt{2E^2} = \sqrt{2}E$

Case (c): Here we see that four identical positive charges are placed at all the four corners of the square. They exert a field of the same magnitude in directions as shown in the diagram. They end up balancing their diagonal charges since the field exerted by a diagonal pair is equal and opposite in nature and end up cancelling each other out,
$E_{resultant} = 0$

Case (d): We have three identical positive charges that are placed in such a way that two form a diagonal pair. The electric fields exerted by the diagonal pairs are equal and opposite in nature and get cancelled out but the remaining one exerts a field equivalent to field exerted by the single charge here, i.e.,
$E_{resultant} = E$

Case(e) we see that we have a diagonal pair of equal and opposite charges. The resultant electric field will be the superposition of the additive diagonal-charge fields ($E+E = 2E$) and the lone positive charge field (E), which will now be aligned perpendicularly.
$E_{resultant} =\sqrt{E_1^2+E_2^2+2E_1E_2cos\theta} = \sqrt{(2E)^2 + E^2 +2(2E)(E)(0)} = \sqrt{5E^2} = \sqrt{5}E$

We can now rank the magnitudes of the resultant electric fields in decreasing order as follows:
$(e) > (b) > (a) = (d) > (c)$

Note:
Always remember that field lines are directed away from positive charges and towards negative charges. The electric field lines are mere virtual representations of the direction of the electric field, and the direction of the electric field will be tangential to the point that they pass through. Field lines are just imaginary tools that we use to trace the paths along which an imaginary test unit charge would move when free, and the presence of an electric field is a sure-shot indicator of the presence of some or the other charge in its vicinity. Since the electric field is a vector, it assumes an additive nature provided opposite directions are indicted by a negative sign. This is how we were able to eliminate and cancel out identical and opposite field strengths in a few cases discussed above.