Question

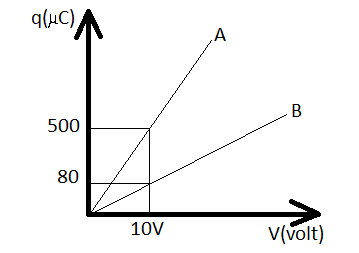
Figure shows charge (q) versus voltage (V) graph from series and parallel combination of two given capacitors. Determine the capacitances.

(A) $50\mu F$ and $30/muF$
(B) $20\mu F$ and $30/muF$
(C) $60\mu F$ and $40/muF$
(D) $40\mu F$ and $10/muF$

Answer 1

Hint In the figure a charge (q) versus voltage (V) graph from series and parallel combination of two capacitors is given. In order to find out the value of the two capacitors, we must use the formula $q = cV$, where q is the charge of the capacitor, V potential difference across two plates and c is the capacitance.

Complete step by step answer
We know that the charge q stored on either plate of a capacitor is directly proportional to the potential difference V across two plates, $q = cV$ where q is charge of the capacitor, V potential difference across two plates and c is the capacitance.
Here the slope of the graph will give capacitance. Now we have to determine capacitance for series and parallel combination.
In series combination,
$\dfrac{{{C_1}{C_2}}}{{{C_1} + {C_2}}} = \dfrac{q}{V}$
$\Rightarrow \dfrac{{{C_1}{C_2}}}{{{C_1} + {C_2}}} = \dfrac{{80}}{{10}}$
$\Rightarrow \dfrac{{{C_1}{C_2}}}{{{C_1} + {C_2}}} = 8 \times {10^{ - 6}}F$……. (i)
In parallel combination,
${C_1} + {C_2} = \dfrac{q}{V}$
$= \dfrac{{500}}{{10}}$
$= 50 \times {10^{ - 6}}F$
Putting the value of ${C_1} + {C_2}$ in equation (i) we get ${C_1}{C_2} = 400 \times {10^{ - 6}}F$
Therefore, capacitance in parallel should be 50/muF & capacitance in series must be 8μF.
It is only possible when ${C_1} = 10\mu F$ and ${C_2} = 40\mu F$

hence option D is correct.

Additional Information $q = cV$, here c is a constant of proportionality called the capacitance of the capacitor. The SI unit of capacitance is farad. 1 Farad = 1 coulomb/volt. The capacitance of a capacitor depends upon the area of the plates, the distance between the plates and the medium between them.

Note Whenever these types of questions appear, first thoroughly examine the graph. From the graph it can be easily determined that the slope of the graph gives capacitance as X and Y-axis represent voltage and charge respectively. Then determine the capacitance for series and parallel combination separately.